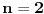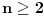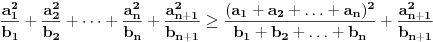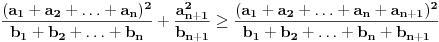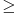 . Resicu prvi problem, jer nisam neki veliki ljubitelj euklidske geometrije. Dakle, zelimo da pokazemo da je
. Resicu prvi problem, jer nisam neki veliki ljubitelj euklidske geometrije. Dakle, zelimo da pokazemo da je 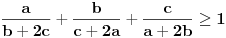 . Naime, vazi
. Naime, vazi 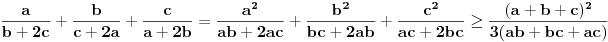 . Ova nejednakost sledi iz nejednakosti
. Ova nejednakost sledi iz nejednakosti 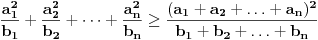 za realne brojeve
za realne brojeve 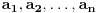 i
i  , koja se moze pokazati indukcijom. Na kraju
, koja se moze pokazati indukcijom. Na kraju 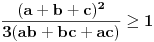 sledi iz
sledi iz 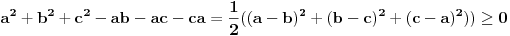 .
.Leonardo da Vinči
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.




 Re: potreban dokaz nejednakosti sa realnim brojevima
Re: potreban dokaz nejednakosti sa realnim brojevima