• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 14.04.2024. Re: Gde je Kejt? (samo pogrešni odgovori) 21.02.2002. Ajzenštajnov kriterijum 22.10.2002. Polinomi 15.12.2003. Nalazenje svih korena polinoma ? 05.04.2004. Gausov interpolacioni polinom i procena greske - .. 12.04.2004. Templejtski polinom i mnozenje 17.05.2004. Langrage-ov interpolacioni polinom! 22.05.2005. Rastavljivost polinoma trećeg stepena 24.09.2005. minimalni polinom 26.10.2005. Prenosna f-ja bipolarca sa z. emiterom Navigacija Brisanje liste Aktuelne teme u ovom forumu: Projekcija tela na ravan trokut za vi osnovne Geometrija-trokut Trokut sa 2 poznate stranice Dokaz teoreme tablicnog limesa? - (sin.. Izbor modula na fakultetu Pomoc oko pronalazenja knjige za predm.. Osmougao, dvanaestougao, šestougao ... Pitanje iz matematike: Presek Jedna nejednakost Transcendentnost brojeva Ludi šeširdžije, druga klapa Logaritamska nejednacina tmf Kombinatorika: n-ta permutacija od ele.. Problem sa razumevanjem i primenom mat.. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

Nuh Privatnik Član broj: 284549 Poruke: 27 *.dynamic.isp.telekom.rs. Profil Komplikovani Polinom 05.07.2011. u 10:45 - pre 155 meseci Dat je polinom Q(x) sa celobrojnim koeficientima da li postoji prirodan broj n takav da je p(1)+p(2)+...+p(n) deljiv sa 1001? Kako se ovo nalazi kako se ispituje da li ima takav broj, nemam nikakvu ideju. Odgovor na temu

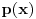
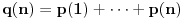
Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8632 89.216.32.* +2790 Profil Re: Komplikovani Polinom 05.07.2011. u 11:34 - pre 155 meseci Pretpostavljam da je zadatak trebao da glasi ovako: Dat je polinom sa celimk koeficijentima. Da li postoji prirodan broj takav da je deljivo sa 1001? Pokušaj najpre da dokažeš da je funkcija polinomna i da je vrednost tog polinoma u tački 0 jednaka 0. Onda stavi da je . 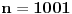Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nuh Privatnik Član broj: 284549 Poruke: 27 *.dynamic.isp.telekom.rs. Profil Re: Komplikovani Polinom 05.07.2011. u 12:09 - pre 155 meseci @Nedeljko Moze jos malo pomoci? Kako se dokazuje da je funkcija polinomna? Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8632 89.216.32.* +2790 Profil Re: Komplikovani Polinom 05.07.2011. u 12:58 - pre 155 meseci Neka je . Lako se dokazuje da je polinom stepena (vodeći član mu je ). Indukcijom po se dokazuje da je . Takođe, indukcijom po stepenu polinoma sa celim koeficijentima dokazuje se da postoje jedinstveni celi brojevi takvi da je . Odatle je , odakle deli . Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nuh Privatnik Član broj: 284549 Poruke: 27 *.dynamic.isp.telekom.rs. Profil Re: Komplikovani Polinom 05.07.2011. u 13:08 - pre 155 meseci Treba li sad da se stavi vrednost za n=1001. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8632 89.216.32.* +2790 Profil Re: Komplikovani Polinom 05.07.2011. u 13:33 - pre 155 meseci Naravno. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nuh Privatnik Član broj: 284549 Poruke: 27 *.dynamic.isp.telekom.rs. Profil Re: Komplikovani Polinom 05.07.2011. u 13:45 - pre 155 meseci Aha,evo da li sam dobro uradio. za , iz cega ocigledno sledi da je ,,deljivo sa 1001. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8632 89.216.32.* +2790 Profil Re: Komplikovani Polinom 05.07.2011. u 13:53 - pre 155 meseci Da. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nuh Privatnik Član broj: 284549 Poruke: 27 *.dynamic.isp.telekom.rs. Profil Re: Komplikovani Polinom 05.07.2011. u 14:22 - pre 155 meseci Nedeljko hvala puno na pomoci!!!! Odgovor na temu