Analitička geometrija-zadatak

Odrediti prave a i b tako da A(0,4) pripada a , B(5,0) pripada b tako da je prava s : 2x-2y-1=0 simetrala ugla koji obrazuju prave a i b.

Kroz pravu A može se postaviti normala na s i naći tačka presjeka D.Zatim naći tačku A' tako da je D sredina duži AA' te preko tačkaka B i A' napisati jednačinu prave b.Isti postupak ponoviti i za pravu a.Pitanje je kako se može drugačije to brže rješiti?

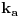
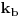
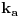
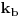
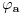
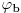
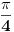
Možeš recimo da nađeš relaciju između i (gde su i koeficijenti pravca pravih i , a i uglovi koje prave i zaklapaju sa x-osom. Pošto simetrala ima nagib , to je





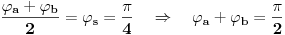
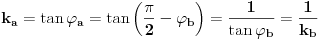
Jednačine pravih i bi bile





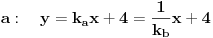
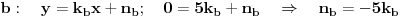
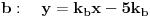
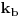
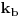
Nađeš prvo presek pravih i , dobićeš u funkciji od . Isto tako nađeš presek pravih i , dobićeš takođe u funkciji od . Sada ta dva dobijena izraza izjednačiš (jer ti preseci treba da se poklapaju) i dobićeš .

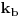
Inače radio sam na oba načina - i na ovaj koji si napisao i na ovaj koji sam sad predložio - i uvek dobijam da ugao koji obrazuju prave i ne postoji, tj. dobijam da se teme tog ugla nalazi u beskonačnosti, odnosno da prave i moraju biti paralelne sa pravom .

Mozda sam pogrešno postavio provjericu.U svakom slučaju hvala na odgovoru dao si mi jednu ideju.