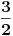Verovatno postoji i neko rešenje u kojem se koristi manje snažan aparat (ovo što ćeš sad videti ti dođe otprilike kao gađanje muve topovskim đuletom) ali zašto ne koristiti ono što nam matematika pruža, pogotovo ako na prvi pogled znaš da ova metoda ne može da omane kod sličnih zadataka. Da ne dužim priču, rešenje ide ovako:
Neka je
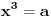
,
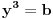
,
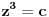
. Očigledno je da važi
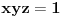
. Na osnovu Mjurhedove nejednakosti (imaš negde na ES-u temu o njoj, ako ti nešto oko same nejednakosti ne bude jasno zamolio bih te da pitaš na toj temi a ne ovde, da ne bi došlo do mešanja diskusija) imamo:
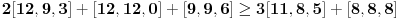
(da ne objašnjavam sad šta predstavljaju ove uglaste zagrade, shvatićeš to kad naučiš Mjurhedovu teoremu).
Razlaganjem ovoga dobijamo:
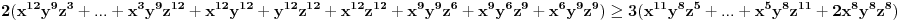
Sad koristimo činjenicu da je
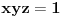
i ovo svodimo na sledeće:
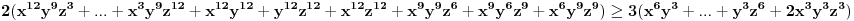
Jednostavno vratimo početna slova i dobijamo:
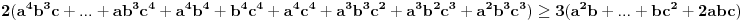
Faktorizacijom ovih izraza dobijamo sledeće (usput možemo desnu stranu pomnožiti sa
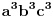
):
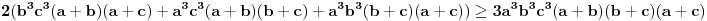
I za kraj, podelimo sve sa
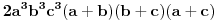
, što nas vodi do
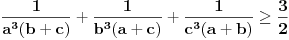
što je i trebalo dokazati.
Ljubičice crvena, što si plava kô zelena trava.
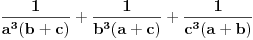 ≥
≥