Jedina greska u mom postu je sto sam slucajno napisao x^2, a u stvari je trebalo da stoji x...
Prvo kao rezultat deljenja dobijete x^2, i onda je x^2*(x^2+4x+6)=x^4+4x^3+6x^2. Kada to oduzmete od x^4+ax^2+b dobije se -4x^3+(a-6)x^2+b. Dalje se deljenjem dobija -4x, pa je -4x*(x^2+4x+6)=-4x^3-16x^2-24x. Kada se to oduzme od -4x^3+(a-6)x^2+b, dobije se (a+10)x^2+24x+b. Opet deljenje i oduzimanje, i dobije se da je rezultat deljenja x^2-4x+(a+10), a ostatak (a+10)x^2+24x+b-(a+10)(x^2+4x+6)=(24-4a-40)x+(b-6a-60), pa iz toga sledi da je
-4a-16=0, tj. a=-4 i
b-6a-60=0, tj. b=36,
pa je a+b=36-4=32.
Nemojte mi zameriti sto nisam dokazao da je 36-4 stvarno 32

E da, jesam li napomenuo da je tacan tekst zadatka:
Ako je x^2 + 4x + 6 faktor od x^4 + ax^2 + b, tada je a + b jednako :..., tj. pogresno je Petar napisao tekst...
 http://prijemni.etf.bg.ac.yu/resenja/2007/matematika.pdf, zadatak broj 16
http://prijemni.etf.bg.ac.yu/resenja/2007/matematika.pdf, zadatak broj 16
There exists only 10 kind of people in the world; those who understand binary numbers and those who don't understand binary numbers.
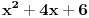 faktor
faktor 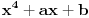 , tada je
, tada je 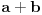 jednako:
jednako: