U pravu si. To se može dokazati na nekoliko različitih načina čak relativno brzo, ali sve one koriste metode više matematike pa sam to koristio kao činjenicu bez navođenja dokaza. Ako se ne varam qzqzqz rešava ovakve zadatke radi pripreme za takmičenje u srednjoj školi, a na svakom takmičenju će prihvatiti samo navođenje toga bez dokaza (zapravo, ne bi moralo da se dokaže ni da je tražena kriva kružnica već je dovoljno i to navesti kao poznato, ali od viška glava ne boli).
No, ipak evo i jednog dokaza koji to popravlja, nešto je duži ali za njegovo razumevanje dovoljno je poznavanje elementarne geometrije i nešto malo graničnih vrednosti.
Na osnovu
Leme 1 zaključujemo da je dovoljno razmatrati krive koje ograničavaju konveksnu površ. Neka je

jedna takva površ, i neka je
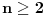
prirodan broj. Postavimo tačke

po ivici

tako da je dužina krive između bilo koje dve uzastopne tačke
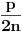
(gde je

zadati obim). Neka je

mnogougao dobijen spajanjem uzastopnim tačaka

. Nacrtajmo pravilan

-ugao
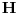
sa centrom
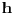
i temenima

stranica dužine
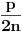
. Neka su
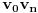
i
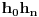
paralelne i horizontalne tako da su
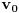
i
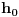
desno, i neka temena oba mnogougla idu u smeru suprotnom kazaljci na satu. Nacrtajmo sve duži
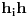
, i iz svake tačke
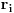
povucimo polupravu koja ima isti pravac i smer kao
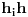
. Ako se
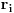
i
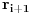
seku u tački
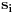
označimo
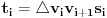
, u suprotnom neka je
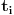
duž
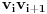
. Sada ćemo pokazati dve stvari:
1)
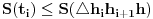
(gde je

površina);
2)
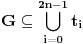
1) Dovoljno je da posmatramo samo trouglove
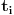
(jer duži imaju površinu

). Dužina duži
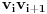
je najviše
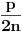
što je i dužina duži
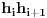
, pa možemo povećati trougao
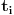
dok se ove dve dužine ne izjednače. Postavimo ih tako da im je ta stranica zajednička. Prema konstrukciji, naspramni ugao im je isti, pa sve četiri tačke leže na jednoj kružnici. Međutim, pošto je
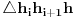
jednakokraki, njegova visina na osnovicu je bar jednaka odgovarajućoj visini drugog trougla, pa mu je i površina bar jednaka površini trougla
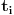
.
2) Pretpostavimo suprotno, tj. da postoji tačka
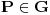
koja ne pripada ni jednoj figuri
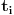
. Prava
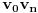
deli figuru

na dva dela, recimo
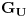
i
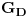
(gornji i donji), i neka
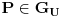
(drugi slučaj se rešava analogno). Povucimo horizontalnu liniju usmerenu nadesno

kroz

, i neka su temena
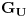
koja leže iznad

upravo
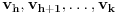
(dakle,

sa svoje desne strane seče duž
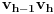
a sa leve
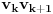
). Za
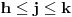
nazovimo još i
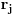
"desni" ako seče

desno od

, i "levi" ako seče

levo od

. Pošto su prema konstrukciji sve poluprave
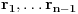
usmerene nadole, svaka od njih je leva ili desna. Dalje možemo razlikovati tri slučaja:
a)
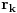
je desni.
Pokazaćemo da
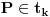
. Neka je
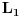
horizontalna prava kroz
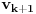
. Poluprava
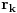
seče
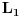
desno od
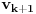
. Pošto je
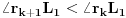
, sledi da se
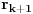
i
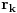
seku ispod
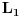
, pa i ispod

. Dakle,
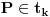
.
b)
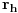
je levi.
Slučaj se radi analogno prethodnom.
c)
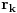
je levi, a
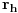
je desni.
Neka je
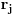
desni takav da je
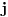
maksimalno moguće. Tada je
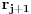
levi. Duž
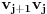
se nalazi iznad

, a pošto je
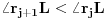
sledi da se
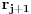
i
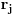
seku ispod

, pa
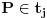
.
Iz 1) i 2) imamo:
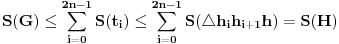
Posle svega ovoga sledi ključan zaključak: ako uzmemo dovoljno veliko

biće
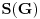
dovoljno blizu
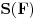
, a
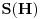
će dovoljno dobro aproksimirati površinu kruga obima

, čime je dokaz završen.
Da napomenem da je problem nalaženja krive konstantnog obima koja ograničava maksimalnu moguću površinu u literaturi poznat pod imenom
izoperimetrijski problem,
izoperimetrijska nejednakost ili
izoperimetrijska teorema.
Ljubičice crvena, što si plava kô zelena trava.