Integral sam delio pre prve smene zato što smena tipa
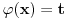
(koju sam ja primenio, s tim što mi je
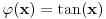
) mora da bude
monotona na intervalu na kojem se integriše. Dobro, to važi za
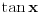
, ali, sa druge strane,
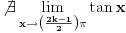
, jer je
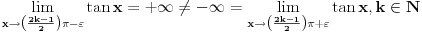
. U svakom slučaju, po teoriji ne bi trebalo da se dobije različit rezultat samo zbog podele integrala na dva dela.
Inače, mislim da funkcija
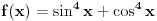
nema (bar ne
realne) nule, pa zato nema ni singulariteta.
Posle druge smene dobija se
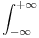
, pa sam podelio integral da bih ga sveo na integrale sa po jednom „tačkom

“.
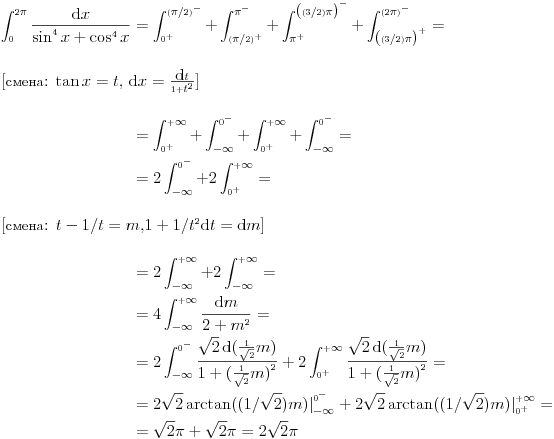
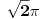 )
)