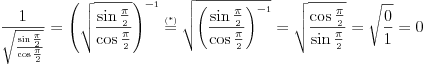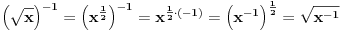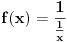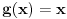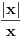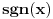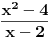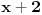[es] - Nesvojstveni integral

Cabo
Lokanje u bircuzu

Član broj: 10942
Poruke: 261
*.beotel.net

Profil

Nesvojstveni integral - deliti ili ne?

^{24.01.2004. u 20:43}

Ovo sam našao u Radenovićevoj zbirci:

E, sad, problem je što se u teoriji kaže da je nesvojstven onaj integral
čija je podintegralna funkcija definisana na poluzatvorenom
intervalu, npr.

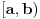, tj. nije definisana u tački

. Ovde funkcija

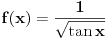nije
definisana u dve tačke:

(jer je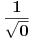

nedefinisano), i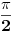

(jer je

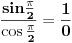
nedefinisano), dakle presek domena funkcije

i segmenta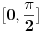

je interval

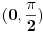. Mislim da nema veze što je

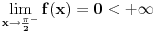, jer se
pre toga integral mora podeliti na dva integrala:

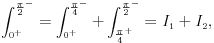
gde je

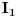singularitet za

, a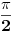

singularitet za

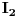. Tek onda se može ispitivati granična vrednost
funkcije za svaki od tih integrala posebno.

Da li sam u pravu? Da li je Radenović malo „skratio“ postupak koji ne
bi trebalo skraćivati?

Unapred hvala,
Cabo

[Ovu poruku je menjao Cabo dana 25.01.2004. u 12:52 GMT]

Kliknite da vidite kako da pišete matematičke formule u [tex]\TeX[/tex]-u bez slanja slika

^{24.01.2004. u 20:43}

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 479
*.4.EUnet.yu

Sajt: www.geocities.com/darkoso..

Profil

Re: Nesvojstveni integral - deliti ili ne?

^{24.01.2004. u 22:17}

U pravu si da prvi integral ima dva singulariteta, ali to kaže i Radenović. Samo dodaje da je druga tačka "prividni" singularitet, pa tako dalje radi kao da nije... Možeš zamislti da je funkcija dodefinisana u pi/2 sa 0, pa imaš poluotvoreni interval...

^{24.01.2004. u 22:17}

Cabo
Lokanje u bircuzu

Član broj: 10942
Poruke: 261
*.beotel.net

Profil

Re: Nesvojstveni integral - deliti ili ne?

^{25.01.2004. u 09:53}

Mislim da je cela stvar u ovome:

Mislio sam da bi moglo da bude problematično jedino mesto označeno zvezdicom. Ali, to je dozvoljeno, jer je:

Dakle, nema smisla govoriti o graničnoj vrednosti kada se algebarskom transformacijom može dobiti konačan broj. Ergo, Radenović nije trebalo ni da računa graničnu vrednost, već samo da konstatuje ovu jednakost. Uh! :-P

Hvala,
Cabo

Kliknite da vidite kako da pišete matematičke formule u [tex]\TeX[/tex]-u bez slanja slika

^{25.01.2004. u 09:53}

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 479
*.ptt.yu

Sajt: www.geocities.com/darkoso..

Profil

Re: Nesvojstveni integral - deliti ili ne?

^{26.01.2004. u 08:44}

Ne može to baš tako, jer, na žalost, funkcije

nisu identične. f(x) nije definisana u nuli, dok g jeste. Bez obzira što one imaju jednake vrednosti za sve ostale vrednosti argumenta.
Ako ti ovo bode oči, pogledaj sledeće primere :

...

^{26.01.2004. u 08:44}