Neka je
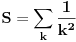
. S konvergira pošto je niz
parcijalnih suma rastući i sa gornje strane ograničen ako ništa drugo,
a ono bar vrednošću
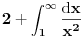
.
Zato možemo da rastavimo na:
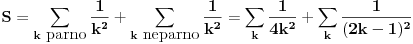
. Obe ove sume konvergiraju iz sličnog razloga
kao i

pa se suma može rastaviti.
Dalje imamo:
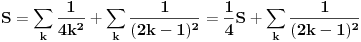
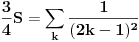
Ovde se primenjuje inženjersko pravilo: ako neće redovi, onda 'oće
Furijeova transformacija. :)
Posmatramo funkciju
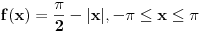
koja je periodična tako da je
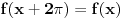
.
Da skratim diskusiju reći ću vam da je ova funkcija parna i sa
srednjom vrednošću 0, pa je njen razvoj u Furijeov red samo:
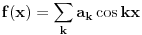
, gde su koeficijenti
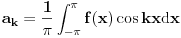
.
Kada sračunate gornji integral, dobija se:
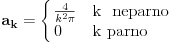
pa je cela funkcija:
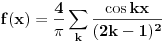
Ako stavimo

dobijemo:
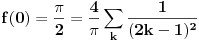
iliti
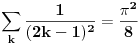
A ako se ubaci u polaznu sumu imamo:
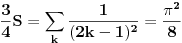
odnosno:
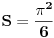
f
(uz ,,malu`` pomoć prof. dr Dobrila Tošića i njegove knjige
Matematika III :) )
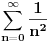
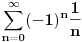 zamenim 1 sa
zamenim 1 sa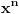 pa trazim f(x) i kad je nadjem,npr. log(1+x) zamenim x sa 1 i dobijem sumu.Ako to radim sa prvim slucajem dobijam jako cudan integral (pretpostavljam neresiv).Zna li neko kako???
pa trazim f(x) i kad je nadjem,npr. log(1+x) zamenim x sa 1 i dobijem sumu.Ako to radim sa prvim slucajem dobijam jako cudan integral (pretpostavljam neresiv).Zna li neko kako???