Majklson-Morlijev eksperimentPretpostavimo dakle jedan koordinatni sistem u kome važe Njutnovi zakoni mehanike, Njutnov zakon gravitacije i Maksvel-Hercove jednačine elektrodinamike. Nazovimo ga osnovni sistem.
Šta je koordinatni sistem? To je jednoznačno pridruživanje tačkama prostorvremena četvorki realnih brojeva, to jest injektivno preslikavanje prostorvremena u
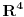. Neka je 
osnovni sistem. Izaberimo bilo koju bijekciju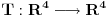 
(dovoljna je čak i injekcija). 
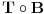je takođe jedan koordinatni sistem. Drugim rečima, možemo dogovorno definisati koordinate neke prostorvremenske tačke tako što prvo odredimo koordinate te tačke u osnovnom sistemu, pa tu četvorku realnih brojeva transformišemo preslikavanjem 
i to što dobijemo prihvatimo kao koordinate te prostorvremenske tačke. To je takođe nekakav koordinatni sistem koji je sa osnovnim povezan transformacijom .Sisteme koji su povezani sa osnovnim Galilejevim transformacijama nazovimo Galilejevim transformacijama, a sisteme koji su sa osnovnim povezani Lorencovim transformacijama nazovimo Lorencovim sistemima. To je moguće jer su sve Galilejeve i Lorencove transformacije bijekcije
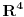na sebe samog, odnosno nema nikakvih prepreka u istovremenom razmatranju Galilejevih i Lorencovih sistema.Njutnovi zakoni mehanike i Njutnov zakon gravitacije, obzirom da važe u osnovnom sistemu i da su Galilej invarijantni, važe takođe u svim Galilejevim sistemima. Maksvel-Hercove jednačine elektrodinamike obzirom da važe u osnovnom sistemu i da su Lorenc invarijantne, važe takođe u svim Lorencovim sistemima.
Zamislimo sada laboratoriju koja se u odnosu na osnovni sistem kreće nekim vektorom brzine
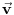uz jedini uslov da je 
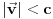i pretpostavimo da laboratorija izvodi eksperiment u kome figurišu samo Maksvel-Hercove jednačine. U Lorencovom sistemu koji se u odnosu na sonovni kreće istim vektorom brzine laboratorija miruje i u njemu takođe važe Maksvel-Hercove jednačine, pa laboratorija ne može da izmeri apsolutno kretanje jer će rezultat biti potpuno isti kao da je laboratorija mirovala u osnovnom sistemu.Zaključak: Ako u eksperimentu (uključujući opis rada instrumenata i proces merenja i sve ostalo) učestvuju samo zakoni koji su invarijantni u odnosu na istu grupu transformacija (recimo, Galilejevu ili Lorencovu), onda se apsolutno kretanje tim eksperimentom ne može detektovati. Da bi se dtektovalo (eventualno) apsolutno kretanje, eksperiment mora da uključuje i pojave koje nisu Galilej invarijantne i pojave koje nisu Lorenc invarijantne, to jest osim osnovnog sistema i onih koji miruju u odnosu na njega postoje i drugi sistemi u kojima važe Maksvel-Hercove jednačine, kao i treći sistemi u kojima važe Njutnovi zakoni mehanike i Njutnov zakon gravitacije, ali nijedan sistem u kome važi sve to istovremeno (osim osnovnog i onih koji miruju u odnosu ja njega), pa je on samo na taj način privilegovan.
Majklson-Morlijev eksperiment je zasnovan samo na svetlosnim pojavama, koje su elektromagnetne i time opisane Maksvel-Hercovim jednačinama, koje su sve Lorenc invarijantne, pa pošto sve važe u Lorencovom sistemu koji se kreće zajedno sa Zemljom, kretanje se ne može detektovati i takav ishod je bio jedini mogući.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
