Evo malo opštijeg stava:
Za svako
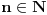
važi:
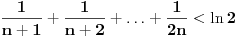
.
Dokaz.
Posle logaritmovanja i sređivanja poznate nejednakosti:
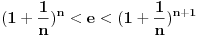
dobijamo ekvivalentnu nejednakost:
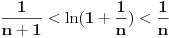
Sada imamo niz nejednakosti:
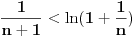
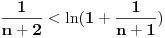

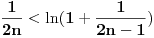
Kada ih saberemo, dobijamo:
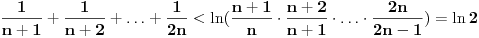
.
Lako se može pokazati da je
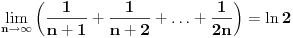
pa je data procena ujedno i najbolja moguća.
Jasno je da mora biti
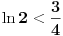
(jer je
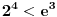
).
@Sasa A:
Koji je bio tvoj pristup rešenju?
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.