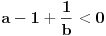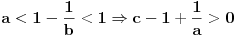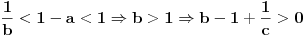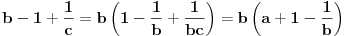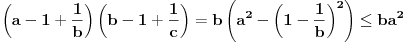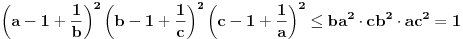Na pretraživaču
www.google.com ukucavši Mathematic Olympiad sam uspeo da pronađem ove zadatke. To su dva zadatka sa matematičke olimpijade 2000. godine. Međutim, ni na jednom od ponuđenih rezultata pretraživača nisam našao rešenja. Ali, profesor Hojoo Lee, koji ima velikog udela u sastavljanju zadataka za olimpijade je izneo određene teoreme, među kojima je i Euler's Theorem. (Dakle, ja ne znam zvanična rešenja tih zadataka, mada verujem da se ovo rešenje donekle i poklapa sa onim zvaničnim.) Njih ima više, ali ona koja mi koristi da uradim prvi zadatak glasi: Neka su x, y i z takvi brojevi da je x,y,z > 0. Tada važi: (x+y-z)(x+z-y)(y+z-x)<=xyz. Korišćenjem toga lako dolazimo do rešenja za prvi zadatak:
Uvedimo smenu: a=x/y, b=y/z i c=z/x (x,y,z > 0 ). Tada je: (x/y-y/y+z/y)(y/z-z/z+x/z)(z/x-x/x+y/x)<=1. Odavde dobijamo (x+z-y)(y+x-z)(z+y-x)<=xyz. (Uvedena smena je moguća, jer je abc=1.)
Kako sam rekao da nemam rešenja ovih zadataka, zamolio bih te da okačiš rešenje drugog, jer i nisam uspeo dokazati da taj broj postoji, mada sam ubeđen da postoji. Sada evo još jednog zadatka (ako imaš bilo kakvo rešenje, tvoje ili zvanično, molim te okači).
Zadatak: Mađioničar ima 100 karata koje raspoređuje u tri kutije: crvenu, belu i plavu, tako da svaka sadrži bar jednu kartu. Njegov pomočnik izabere dve od tri kutije, po jednu kartu iz svake i saopšti zbir izabranih karata. Kada čuje traženi zbir, mađioničar utvrđuje kutiju iz koje nije izabrana karta. Koliko načina postoji da se sve karte stave u kutije tako da ovaj trik uvek uspe? (Dva načina su različita ukoliko je najmanje jedna karta stavljena u drugu kutiju.)
If you don't live for something, you will die for nothing.




 Zadaci s olimpijada
Zadaci s olimpijada