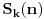
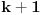
pošto smo videli u prethodnom razmatranju da je polinom po stepena , mogli bismo ga tražiti preko metoda neodređenih koeficijenata.
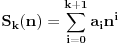
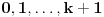
Znači uzmemo da je , i krenemo da umesto zamenjujemo vrednosti:. Tako dobijemo sistem linearnih jednačina, pa ako je dovoljno malo možemo da ga rešimo i nađemo koeficijente .
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
[tex]1^k+2^k+...+n^k, k \in N[/tex]
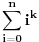za neko 
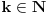. Za k=1,2 znam.
Re: [tex]1^k+2^k+...+n^k, k \in N[/tex]
