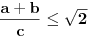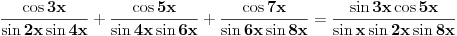darkosos je prvi odlicno poceo zakljucivati , ali mu je malo dosadilo
tjerati dalje pa je onda zbrzio onaj zavrsetak i normalno: promasio.
-Sad malo da odgovorim na one predhodne kritike da , kao nije dovo-
ljno definisan zadatak pa se moze napraviti beskonacno nekakvih
egzoticnih pozicionih brojnih sistema u kojima se mogu napisati one
cifre.Da , ali sta je sa onom jednacinom koja mora biti ispostovana?
Svi brojni pozicioni sistemi su samo nacin ispisivanja prirodnih brojeva.
Sve brojne i mjesne vrijednosti moraju biti prirodni brojevi sa dodatkom
nule (jer bez nje nema sanse napraviti p.b.s).
Tacno je da nisam naglasio da omjer susjednih poz. vrijednosti nije konstanta
, ali to se lijepo vidi iz one jednadzbe i zelio sam da to sami uocite(zadnje tri
cifre pri zbrajanju).Odmah bi odustali od onih jednadzbi gdje je ukljucen
taj uslov koji ovdje ne vrijedi.(A gdje je to neko zabranio praviti p.b.s
u kojima ne vrijedi taj uslov i kakva je kazna ko napravi prekrsaj?)
Pokusajte pisati prirodne brojeve po ovom sistemu dokle ide.Docicete
do onog : a kad nastupa 100? Dilema,3-lema ,4-lema.....
Kad bi to znali lako bi dalje:1000;10000 ...jel tako?
Probajte na silu a kontrola je ona jednadzba koja sputava divljanje.
(mislim da cete na osnovu logike iz prve rijesiti onu dilemu)
Dakle ovdje je bilo sve uredno definisano.Postoje samo 2 kvake sto
nije mnogo.Tipujem da ce darkosos rijesiti , samo molim ne zavirujte
vise u onu rubriku gdje se uvjezbava tex.
Kad neko rijesi vidjecete da je sve ok.Sistem je simpatican jer ima
ogromnu glavu a fin i precizan rep.
Jako ste me nasikirali pa odoh.....
________________________________
Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500
OK evo prave formule:P=2wft^2 [period]
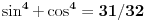 odrediti
odrediti 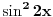
 i
i  katete a
katete a  hipotenuza , dokazati
hipotenuza , dokazati