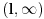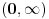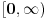Izracunati
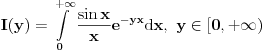 .
.Resenje. Neka je
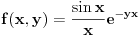 . Dodefinisimo funkciju
. Dodefinisimo funkciju  tako da ona bude neprekidna (na zadatim intervalima):
tako da ona bude neprekidna (na zadatim intervalima):
Dalje,
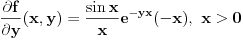 , ali kako vazi i za
, ali kako vazi i za  , to mozemo reci da vazi za
, to mozemo reci da vazi za 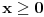 .
.Dakle,
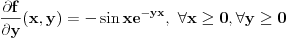 , tj. funkcija
, tj. funkcija 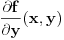 je neprekidna.
je neprekidna.Dalje, treba pokazati da
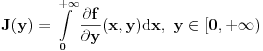 , odnosno
, odnosno 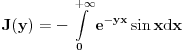 ravnomerno konvergira po
ravnomerno konvergira po  .
.Za
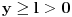 vazi
vazi  (sto (ogranicenje) ne zavisi od
(sto (ogranicenje) ne zavisi od  ), a kako
), a kako 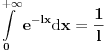 (odnosno konvergira), to prema Vajerstrasovoj teoremi i
(odnosno konvergira), to prema Vajerstrasovoj teoremi i 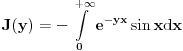 ravnomerno konvergira za
ravnomerno konvergira za 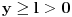 . (ako se ne bismo malo odmakli od nule, imali bismo problem ako hocemo da pokazemo preko Vajerstrasa, jer bi jedino mogli da kazemo da
. (ako se ne bismo malo odmakli od nule, imali bismo problem ako hocemo da pokazemo preko Vajerstrasa, jer bi jedino mogli da kazemo da 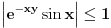 , a integral
, a integral 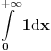 divergira, pa ne mozemo preko Vajerstrasa)
divergira, pa ne mozemo preko Vajerstrasa)Dalje, moze se pokazati da
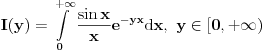 ravnomerno konvergira po
ravnomerno konvergira po  . Naime,
. Naime, 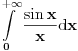 konvergira (u 0 je limes 1, u beskonacnosti Dirihle), a kako ne zavisi od parametra
konvergira (u 0 je limes 1, u beskonacnosti Dirihle), a kako ne zavisi od parametra  on i ravnomerno konvergira po
on i ravnomerno konvergira po 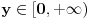 . Dalje, funkcija
. Dalje, funkcija 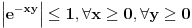 i
i 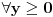 funkcija
funkcija 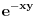 je opadajuca (po
je opadajuca (po 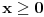 ). Pa su ispunjeni uslovi Abelove teoreme i mozemo reci da
). Pa su ispunjeni uslovi Abelove teoreme i mozemo reci da 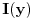 ravnomerno konvergira po
ravnomerno konvergira po  . (primetimo da za uslov teoreme (koja sledi) nam nije potrebno da
. (primetimo da za uslov teoreme (koja sledi) nam nije potrebno da 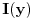 ravnomerno konvergira po
ravnomerno konvergira po  , vec je dovoljno da
, vec je dovoljno da 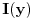 konvergira za bar jedno
konvergira za bar jedno 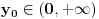 (sto i vazi, cak konvergira i u svim kao sto je upravo pokazano), ali da ce nam kasnije zatrebati ova osobina funkcije
(sto i vazi, cak konvergira i u svim kao sto je upravo pokazano), ali da ce nam kasnije zatrebati ova osobina funkcije 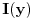 )
)Prema jednoj od teorema (ciji su uslovi provereni u prethodnom delu) vazi
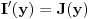 za
za 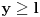 . Dakle, za
. Dakle, za 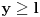 vazi
vazi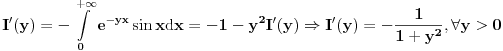 , integral se resava posle dve parcijalne (mozemo reci za
, integral se resava posle dve parcijalne (mozemo reci za 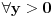 jer je
jer je  bilo proizvoljno (naravno, takvo da vazi
bilo proizvoljno (naravno, takvo da vazi  ))
))Odnosno, dobijamo da je
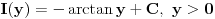 .
.  mozemo naci iz
mozemo naci iz 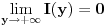 , jer je za
, jer je za 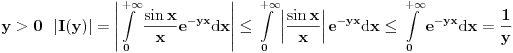 . Dakle, dobijamo da vazi
. Dakle, dobijamo da vazi 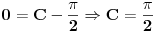 , odnosno
, odnosno 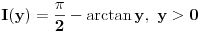 .
.E sad, treba izracunati integral i za
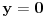 .
.To bi moglo ovako,
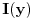 ravnomerno konvergira po
ravnomerno konvergira po 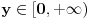 , a
, a 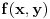 je neprekidna na
je neprekidna na 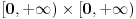 , tako da prema jednoj od teorema vazi i da je
, tako da prema jednoj od teorema vazi i da je 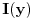 neprekidna na
neprekidna na 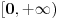 , pa vazi
, pa vazi 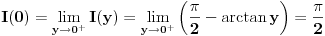 . Pa vazi (kada se sve sklopi) da je
. Pa vazi (kada se sve sklopi) da je 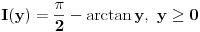 .
.Odavde se moze videti i da je Dirihleov integral
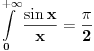 .
.Leonardo da Vinči
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.




 Parametarski nesvojstveni integral
Parametarski nesvojstveni integral