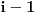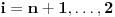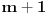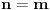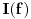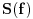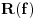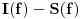Pozdrav svima :)
Spremam usmeni iz numericke analize, pa imam "par" nejasnoca. Nadam se da ce neko od vas moci da mi odgovori :) Neka pitanja ce sigurno biti banalna, ali mi mozak od numerike slabo funkcionise, pa se unapred izvinjavam.
Pa da pocnem :)
Kod interpolacije imamo Vandermondovu determinantu koja je oblika

zanima me kako se dobija desna strana, da li postoji neko posebno pravilo ili je tako Vandermond rekao :D
Dalje, kod osobina podeljenih razlika imamo da je

e sad, meni nije jasno u prvoj zagradi sa cim se mnoze alfe, u izrazu sa desne strane mi je jasno, ali ovo bas i ne. (ovo je jedno od onih glupih pitanja :))
Kod aproksimacije polinomima imamo sistem normalnih jednacina

da li su Yi sa desne strane vrednosti aproksimirane f-je?
Kod resavanja predodredjenog sistema linearnih algebarskih jednacina metodom najmanjih kvarata ima jedan crtez koji mi apsolutno nije jasan, pa bih vas zamolila da mi neko objasni ako moze, bar u kratkim crtama

vidim da su to neke prave i da imamo priblizne vrednosti x* i y* koje formiraju kvadrat, ali mi nikako nije jasno kako se tim crtezom objasnjava ova metoda.
Onda, kod dokaza o konvergenciji metode proste iteracije za resavanje sistema nelinearnih jednacina javlja se korak za dokazivanje Kosijevog niza

Ceo taj postupak mi je jasan, osim poslednjeg koraka, kako je od onog izraza u zagradi nastao razlomak?
Jos samo malo ima, obecavam :D
Kod metode najmanjih kvadrata ne uzimamo

zato sto nije diferencijabilna svugde. E sad glupo pitanje, zasto nije diferencijabilna? :) I da li ce sistem koji budemo aproksimirali metodom najmanjih kvadrata imati m+1 jednacinu sa m+1 nepoznatom ili sa n+1 nepoznatom (mislim da mozete videti sa slike sta je m, a sta n)
I za kraj :) Da li kod kvadraturne formule za Simpsonovu metodu, kada zapocinjemo izvodjenje

treba da sa desne strane bude dodata i greska ili je nepotrebno, posto kod mene u knjizi stoji izraz bez greske?
Unapred vam hvaaala puuuuuuno na odgovoru :)
Pozz,
Milica
p.s. Mozda se jos neceg setim u medjuvremenu :)




 Numericka analiza
Numericka analiza