[es] - Mjurheadova teorema

Nedeljko
Nedeljko Stefanovic

Član broj: 314
Poruke: 2299
*.dial.InfoSky.Net.

Profil

^{27.02.2005. u 21:38}

Tako mi i treba kada brzopleto dajem izjave.

^{27.02.2005. u 21:38}

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3512
*.dialup.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

Profil

Re: Mjurheadova teorema

^{27.02.2005. u 21:47}

Nemoj da se nerviraš, svi grešimo, zato i postoji ovaj forum da možemo razmeniti mišljenja i eventualno jedni drugima skrenuti pažnju na grešku ako se ukaže potreba za tim.

Ljubičice crvena, što si plava kô zelena trava.

^{27.02.2005. u 21:47}

Nedeljko
Nedeljko Stefanovic

Član broj: 314
Poruke: 2299
*.dial.InfoSky.Net.

Profil

Re: Mjurheadova teorema

^{28.02.2005. u 00:15}

Ne nerviram se ni najmanje. Samo sam mogao da proverim tvrdnju pre nego što je napišem.

^{28.02.2005. u 00:15}

Metalnem
Nemanja Mijailovic

Član broj: 6757
Poruke: 184
*.vdial.verat.net.

Profil

Re: Mjurheadova teorema

^{28.02.2005. u 14:22}

Da li se zadatak III moze resavati na sledeci nacin: prvo se pomoze obe strane sa 2(x+z)(x+y)(y+z) i na levoj strani se dobija da je zbir izlozilaca u svim sabircima 2, a na desnoj 3. Zatim sve to kvadriramo, pa levu stranu pomnozimo sa xy+xz+yz. Dobijamo i na levoj i na desnoj strani da je zbir izlozilaca u svim sabircima 6 i onda od toga napravimo nejednakost?

PS: Za ovo sto sam napisao mislim da je x, y ,z > 0. Slucaj kada je jedan od brojeva jednak nuli se lako dokazuje.

^{28.02.2005. u 14:22}

Metalnem
Nemanja Mijailovic

Član broj: 6757
Poruke: 184
213.244.197.*

Profil

Re: Mjurheadova teorema

^{28.02.2005. u 15:56}

Imam i ja jedan zadatak:

^{28.02.2005. u 15:56}

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3512
*.dialup.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

Profil

Re: Mjurheadova teorema

^{28.02.2005. u 19:52}

Citat:

Metalnem:
Da li se zadatak III moze resavati na sledeci nacin: prvo se pomoze obe strane sa 2(x+z)(x+y)(y+z) i na levoj strani se dobija da je zbir izlozilaca u svim sabircima 2, a na desnoj 3. Zatim sve to kvadriramo, pa levu stranu pomnozimo sa xy+xz+yz.

Može, naravno. U sličnim zadacima se često koristi sličan trik kao u zadatku I gde uvedeš nova slova da bi smanjio stepen onoga sa čime množiš (u tom slučaju bi uštedeo kvadriranje onolikog izraza što nije naročito zahvalan posao), međutim to ovde ne može da prođe tako da mora ovako. Reci mi samo zašto bi hteo da posebno ispituješ slučaj kada je neki od brojeva jednak 0 jer je to sve obuhvaćeno Mjurhedovom nejednakosti.

Što se tiče ovog tvog zadatka nisam siguran da li si ga postavio kao primer ili zato što ti treba rešenje, ali u svakom slučaju i on ide trivijalno, kreneš od

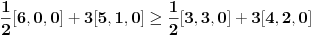
(što je tačno), a to upravo predstavlja razvijeni oblik tvog izraza.

Ljubičice crvena, što si plava kô zelena trava.

^{28.02.2005. u 19:52}

Metalnem
Nemanja Mijailovic

Član broj: 6757
Poruke: 184
*.vdial.verat.net.

Profil

Re: Mjurheadova teorema

^{28.02.2005. u 20:38}

Citat:

Reci mi samo zašto bi hteo da posebno ispituješ slučaj kada je neki od brojeva jednak 0 jer je to sve obuhvaćeno Mjurhedovom nejednakosti.

Da, izvinjavam se, nisam pazljivo procitao jedan od tvojih ranijih postova. A ovaj zadatak je cisto kao primer ako jos nekoga interesuje.

^{28.02.2005. u 20:38}

useer
beograd

Član broj: 98019
Poruke: 38
*.adsl.sezampro.yu.

Profil

Re: Mjurheadova teorema

^{21.06.2006. u 18:29}

iz ovih vasih postova i naravno neke literature sa neta naucio sam mjurheda i sad sam malo pokusavao da ga navezbam i to ide malo po malo ali sve na nekim tezim zadacima...imate li neke zadatke za mjurheda (i ostale teoreme iz nejednakoti)na kojima bih mogao da steknem osecaj za to da bih posle mogao da radim i teze stvari

^{21.06.2006. u 18:29}