Kineska teorema o ostacima precizno glasi ovako:
Neka su

prirodni brojevi koji su u parovima uzajamno prosti i neka su

celi brojevi za koje je
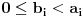
za sve
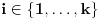
. Tada postoji tačno jedan ceo broj
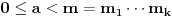
takav da je
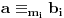
za sve
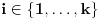
, pr čemu simbol
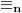
predstavlja kongruenciju po modulu

.
Neka je
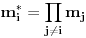
. Budući da je
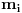
uzajamno prost sa
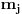
za svako
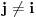
,
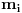
je uzajamno prost i sa njihovim proizvodom
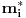
, pa postoje celi nenegativni brojevi
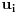
i
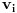
za koje je
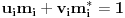
. To, tačno znači da je
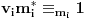
, a samim tim i da za broj
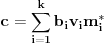
važi
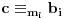
za sve
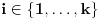
. Ako sada uzmemo da je

nenegativan ostatak pri delenju broja

sa

, broj

će ispuniti tražene uslove. Time je dokazana egzistencija.
Ako bi još neki element
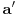
ispunio tra\ene uslove, onda bi broj
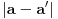
bio deljiv sa
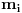
za svako
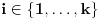
, a samim tim i sa njihovim proizvodom

budući da su brojevi
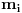
u parovima uzajamno prosti. No, iz
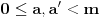
sledi da je
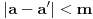
, odakle najzad mora biti
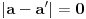
čime je dokazana jedinstvenost.
Ova teorema se primenjuje u Algebri u teoriji konačnih Abelovih grupa, kao i u Logici u dokazu Gedelovih teorema nepotpunosti.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.