U medjuvremenu sam osmislio i algoritam za opsti slucaj permutacija, gde se pojedini elementi mogu i da ponavljaju i on bi izgledao otprilike ovako:
* Sortiramo niz A = [ a[1], a[2], ... a[n] ] u leksikografskom poretku, od najmanjeg ka najvecem.
* Kumulativni brojac permutacija postavimo na nulu (npr. C=0)
* Za svaki unikatni element niza
x definisemo funkciju R(x) koja oznacava broj ponavljanja elementa
x u nizu A. Na primer, za niz [ 1, 2, 2, 2, 3, 3, 4, 4, 4, 4 ] funkcija R ce izgledati otprilike ovako: R = { 1 -> 1, 2 -> 3, 3 -> 2, 4 -> 4 }, jer je skup unikatnih elemenata niza A skup B={ 1, 2, 3, 4 }.
* Za svaki element
x skupa unikatnih elemenata (B) odredimo ukupan broj permutacija ciji je vodeci element
x. Taj broj se odredjuje tako sto iz originalnog niza izbacimo prvu instancu elemnta
x i izracunamo ukupan broj permutacija tog "okrnjenog" niza. Znaci, pocinjemo recimo od jedinice, za koju pretpostavimo da je vodeca - iz niza A izbacimo 1 i ostaje nam [2, 2, 2, 3, 3, 4, 4, 4, 4 ]. Ukupan broj permutacija je 9!/(3!*2!*4!). Primer Python koda kojim se to racuna bi otprilike izgledao ovako:
Code (python):
def nPerm (array):
np = fact(len(array)) # Broj permutacija bez ponavljanja elemenata
for elem in set(array): # Za svaki unikatni element niza "array" ...
np = np / fact(array.count(elem)) # Podeli np faktorijelom broja ponavljanja elemnta
return np
Sto je programska interpretacija poznate formule:
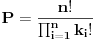
gde su k{i} brojevi ponavljanja elemenata iz posmatranog niza.
* Proverimo da li je zadati redni broj permutacije (r) manji od C. Ako jeste, pronasli smo vodeci element, on se garantovano nalazi u intervalu (C, P). Ako nije, kumulativnom brojacu C dodajemo broj P (C = C+P) i prelazimo na sledeci element skupa B ... postupak ponavljamo sve dok je r > C.
* Kada r postane manje od C - nasli smo vodeci element. Izbacimo prvu instancu vodeceg elementa iz originalnog niza A i ponavljamo postupak nad smanjenim nizom A'. Na primer, ako smo pronasli da je vodeci element 2, tada formiramo niz A' = [ 1, 2, 2, 3, 3, 4, 4, 4, 4 ]. Ako smo nasli da je vodeci element 3, tada je A' = [ 1, 2, 2, 2, 3, 4, 4, 4, 4 ].
* Dodamo vodeci element u novi niz - ako je to trojka u prvoj iteraciji cemo dobiti Q = [ 3 ].
* Kompletan postupak rekurzivno ponavljamo nad nizom A'.
* Krajnji rezultat je niz Q, koji ce na kraju ovog rekurzivnog postupka biti popunjen trazenom permutacijom.
Ima tu jos detalja, ali to je u grubim crtama to sto treba uraditi. Entuzijastima ostavljam punu implementaciju, nije tesko.