Pošto neću biti tu narednih par dana a zaista ne umem da smislim neki "odmeren" hint koji ne bi rekao sve ali bi ipak pomogao (zapravo, jedan sam postavio,
http://www.elitesecurity.org/poruka/667448, ali izgleda da niko nije shvatio šta je pisac hteo da kaže), napisaću sad celo rešenje.
Neka je data familija čiji članovi imaju po
elemenata. Dokazaćemo sledeće: ako je
skup takav da je
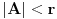
koji je sadržan u beskonačno mnogo skupova iz familije
, onda važi da ili
ima neprazan presek sa svakim skupom iz familije
(u tom slučaju smo završili), ili postoji neki element
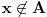
takav da je
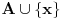
sadržan u beskonačno mnogo skupova iz familije
. Pošto jedan takav skup očigledno postoji (npr.
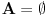
), ako dokažemo ovu tvrdnju onda njenom uzastopnom primenom
puta dobijamo to što se traži (jer skup veličine
sigurno ne može biti sadržan u beskonačno mnogo skupova iz naše familije). Da bismo dokazali tvrdnju, pretpostavimo da neki skup
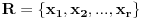
iz date familije nema zajedničkih elemenata sa skupom
. Svaki od onih beskonačno mnogo skupova koji sadrže
ima neprazan presek sa
, znači neko
iz
se sadrži u beskonačno mnogo takvih skupova, iz čega sledi da možemo uzeti
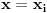
. Ovim je dokaz završen.
Nadam se da se oni što su želeli još malo da razmisle ne ljute što sam odmah objavio celo rešenje. U svakom slučaju, ako ste zainteresovani imate nekoliko svežih zadataka različite težine u
http://www.elitesecurity.org/poruka/667144, a kao i do sada ću s vremena na vreme postavljati slične mozgalice.
Ljubičice crvena, što si plava kô zelena trava.
Re: [Zadatak]: Beskonačna familija konačnih skupova
