Čini mi se da si blizu rešenja, ali mislim da si još uvek pomalo upetljan. Da probam ja to tvoje rešenje da prevedem na matematički jezik pa mi ti reci da li sam dobro razumeo šta hoćeš da kažeš.
Neka je
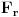
beskonačna familija skupova od po

elemenata koji zadovoljavaju uslove zadatka. Pretpostavimo (indukcijska hipoteza) da za svaku takvu familiju važi tvrđenje. Sada posmatramo familiju
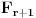
i neka jedan skup iz te familije sadrži elemente
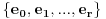
. Očigledno je bar jedan od tih elemenata sadržan u beskonačno mnogo skupova iz familije
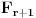
. Neka je to, bez umanjenja opštosti, elemenat
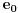
. Sada posmatramo familiju
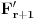
koja se sastoji od skupova iz familije
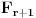
koji sadrže elemenat
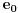
, i posmatramo familiju
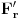
koja se dobija na taj način što iz skupova familije
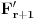
odstranimo element
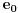
. Prema indukcijskoj hipotezi postoji skup veličine
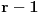
koji ima neprazan presek sa svakim skupom iz familije
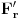
, nazovimo taj skup

. I sada, ako se ne varam, ti tvrdiš da je skup
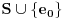
traženi skup za familiju
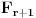
. E tu se već ne mogu složiti sa tobom, ono što mi znamo u ovom momentu je da je skup

traženi skup za familiju
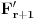
, ali i dalje ne znamo da on ima neprazan presek sa skupovima koji pripadaju familiji
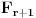
a ne pripadaju familiji
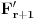
. Da li sam možda negde pogrešio u tumačenju ovog tvog rešenja?
Ljubičice crvena, što si plava kô zelena trava.
 skupova veličine
skupova veličine 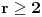 (svi su iste veličine) takva da u njoj ne postoje dva skupa čiji je presek prazan. Dokazati da postoji skup veličine
(svi su iste veličine) takva da u njoj ne postoje dva skupa čiji je presek prazan. Dokazati da postoji skup veličine 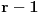 koji ima neprazan presek sa svakim skupom iz familije
koji ima neprazan presek sa svakim skupom iz familije  .
.