Nedeljko ti je u principu odgovorio, samo bih ga malo dopunio.
1) Zaboravio si da napomeneš da su svi a-ovi i b-ovi pozitivni;
2) Način koji si predložio za rešavanje ovog zadatka je dobar s tim što moram da napomenem da ako budeš sličan zadatak rešavao "zvanično" (na nekom kontrolnom ispitu, takmičenju...) kreni suprotnim redosledom od ovog koji si ti naveo, tj. napišeš: "Na osnovu Mjurhedove nejednakosti imamo da je
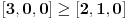
iz čega sledi...". Ovo pričam zbog toga što znam da ti što pregledaju takve stvari vole da zakinu bodove što nisi svugde pisao ekvivalenciju, u principu to ne bi smeli da rade ali ništa te ne košta da napišeš ovako kao što sam rekao. Znači, sebi sa strane skiciraš rešenje, vidiš šta se dobije na kraju, i onda na onom listu što predaješ kreneš odatle pa stigneš do početka, ako razumeš šta hoću da kažem.
3) Možeš da rešiš 95% nejednakosti gde su promenjive ravnopravne, Mjurhed je zakon za takve stvari (iako u 90% slučajeva postoji jednostavnije rešenje primenom AG ili neke slične manje moćne nejednakosti zahvaljujući Mjurhedu uopšte ne moraš da razmišljaš šta sa čim kombinovati, samo izmnožiš sve, poskraćuješ šta možeš i vidiš šta ostaje na kraju). Evo i par primera koji su mi trenutno pali pod ruku (neki mogu i sasvim elementarno ali napisaću ih ovde radi ilustracije Mjurhedove nejednakosti):
I)
http://www.elitesecurity.org/tema/98452 (pošto si ti postavio temu sigurno znaš za ovo, ali neka stoji ovde da i drugi korisnici mogu da vide);
II) Ako su
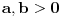
,
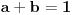
, dokazati
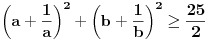
.
III) Za
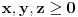
,
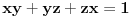
dokazati da važi
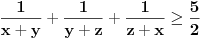
.
IV) Ako
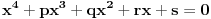
ima 4 realna pozitivna rešenja, dokazati da važi:
a)
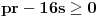
;
b)
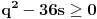
.
Mislim da je dosta za sada.
[Ovu poruku je menjao Bojan Basic dana 27.02.2005. u 15:47 GMT+1]
Ljubičice crvena, što si plava kô zelena trava.