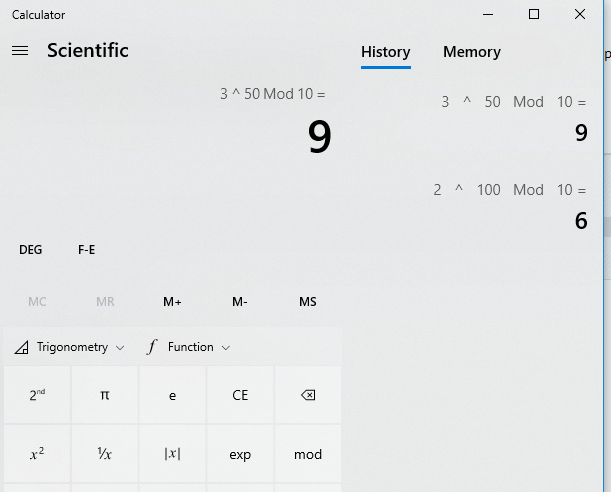
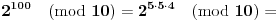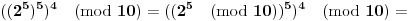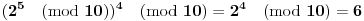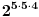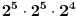Zadatak: Koja je poslednja cifra proizvoda
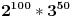 .
.Shvatam da je:
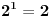
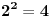
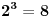
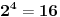
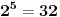 ......
......kao i da je:
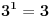
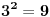
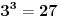
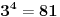
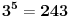 ......
......Dakle, interval je 4 vrednosti, pa se poslednje cifre ponavljaju. I ja kontam da je verovatno resenje, naci poslednju cifru iz
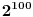 i poslednju cifru iz
i poslednju cifru iz 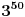 , i poslednja cifra njihovog proizvoda je i poslednja cifra proizvoda sa pocetka zadatka. Ali nemam ideju kako da rastavim ove stepene i sto je najbitnije zasto da ih rastavim bas tako.
, i poslednja cifra njihovog proizvoda je i poslednja cifra proizvoda sa pocetka zadatka. Ali nemam ideju kako da rastavim ove stepene i sto je najbitnije zasto da ih rastavim bas tako. Ako neko ima vremena da pored resenja ostavi i neki slican primer, pa da probam sam da resim.
Unapred hvala svima!!!!




 Poslednja cifra proizvoda
Poslednja cifra proizvoda