Inicijator je ovo potpuno pogrešno povezao sa Geometrijom Lobačevskog, ali se ovo može povezati sa Teorijom distribucija i Dirakovom "funkcijom" (zapravo distribucijom).
Do mnogih dobrih ideja se došlo na matematički protivrečan način, da bi se kasnije stvari "popravile", recimo kada se našlo odgovarajuće okruženje. Znate li recimo kako je Leonard Ojler došao do čuvenog razvoja sinusa u beskonačni proizvod
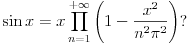
Razmatrao je Tejlorov razvoj sinusa
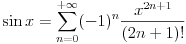
shvativši sinus kao "beskonačan polinom" sa koeficijentom 1 uz x čije su nule jednostruke i jednake
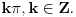
Kasnije je dokazao da ta formula važi u još nekim tačkama, da bi na kraju dao korektan dokaz da ta formula važi u opštem slučaju. Gedel možda ne bi ni došao do svojih čuvenih teorema nepotpunosti da nije pokušavao da formalizuje Rišarov paradoks, ne bi li video šta će iz toga da ispadne. Da li je trebalo grditi Ojlera i Gedela?
Isto tako je i Dirakova "funkcija" bila matematički nekorektno uvedena, ali je davala u Fizici odlične rezultate. Kasnije je pronađen odgovarajući formalizam u kome se sa takvim pojmom moglo raditi. Tamo je ova "funkcija" prestala da bude "funkcija" i postala je distribucija. U Fizici ima jako puno takvih primera. Fizičari najčešće rade na takozvanom fizičkom nivou strogosti, koji je niži od matematičkog. Dirakova funkcija se "proslavila" po tome što je za nju pronađen odgovarajući matematički formalizam, dok za mnoge druge tehnke koje koriste fizičari nije.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Poslednji cifra broja Sqrt(2)
Re: Poslednji cifra broja Sqrt(2)
Re: Poslednji cifra broja Sqrt(2)
