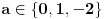Sistem ima rešenje ako i samo ako je rang matrice sistema jednak rangu matrice proširenog sistema.
E sad, na sajtu matematiranje.com je receno da na uokvirenim mestima ne smeju biti nule da bi sistem imao jedinstveno resenje.
Moze li neko da mi objasni zasto jer na sajtu nije objasnjeno.
I kako da uocimo koji je rang matrice sistema a koji rang matrice prosirenog sistema. Na primer koji su rangovi matrice ako su na uokvirenim mestima nule.





 Rang matrice prosirenog sistema
Rang matrice prosirenog sistema