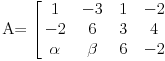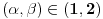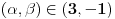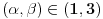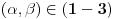Rang transponovane matrice matrice A je jednak rangu matrice A. No, tebi za Kroneker Kapelijevu teoremu ne treba rang transponovane matrice, već proširene matrice.
Koliki je rang matrice

?
Oduzimanjem druge vrste pomnožene sa 3 od treće vrste i zamenom mesta drugoj u četvrtoj koloni dobija se matrica

.
Dakle, rang je 2. Sa druge strane, matrica
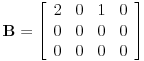
ima rang 1. Matrice A i B se razlikuju samo u poslednjoj koploni, a imaju različite rangove. Znači, rang zavisi od poslednej kolone.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 i
i  je rang matrice A jednak 2?
je rang matrice A jednak 2?