Bio sam u frci sa vremenom, naveo sam ugrubo skicu dokaza, da vidim da li je dobro. Sada ću neke dijelove detaljnije da obrazložim.
Hvala Nedeljko što si me dopunio, nisam stigao sve da napišem.
Da, tako je kako si napisao.
Citat:
Nedeljko:
Kako si zaključio da je skup f(R) prebrojiv? Kako je njegova neprebrojivost u nesaglasnosti sa prebrojivošću N?
Pretpostavimo suprotno, da je f(
R)={f(x)|x
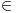 R
R} neprebrojiv.
Tada postoji familija skupova
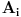
,
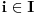
.

je skup indeksa, prema našoj pretpostavci neprebrojiv.
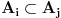
,
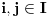
. Jasno je da je
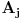
\
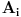
beskonačan skup (u suprotnom ne bi postojao skup
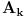
tako da vrijedi
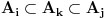
, za svako i i j iz skupa indeksa

). Jasno je da je svaki od ovih skupova beskonačan kao i njihovi komplementi u
N što takođe slijedi iz osobina (
R,<) i definicije funkcije f.
Za svaka dva indeksa i i j iz skupa

,
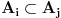
, može se uzeti element
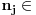 N
N koji pripada skupu
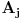
\
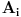
. Na taj način formiran skup {
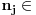 N
N|
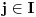
} iz lanca skupova
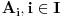
je neprebrojiv.
{
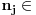 N
N|
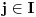
}
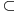 N
N je u kontradikciji sa prebrojivošću skupa
N.
 koja svakom realnom broju pridružuje podskup skupa prirodnih brojeva, tako da za ma koje realne brojeve
koja svakom realnom broju pridružuje podskup skupa prirodnih brojeva, tako da za ma koje realne brojeve  i
i  takve da je
takve da je 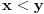 važi
važi 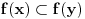 (
( je pravi podskup od
je pravi podskup od 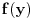 ).
).