Ajde da pokušam da objasnim, mada je dosta teško ovako od nule pa ako ti nešto ne bude jasno slobodno dodatno pitaj.
Neka su
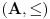
i
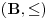
dva dobra uređenja (totalno uređenje je dobro ako svaki njegov neprazan podskup ima najmanji element). Za njih se kaže da imaju isti tip uređenja akko postoji bijekcija
iz
u
takva da za sve
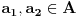
važi
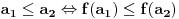
. Dakle, sva dobra totalna uređenja možemo razvrstati u neke kategorije tako da elementi svake kategorije međusobno imaju isti tip uređenja. Predstavnik jedne takve kategorije naziva se ordinalni broj ili skraćeno ordinal. Dakle, ordinal je zapravo neki dobro uređen skup. Prvih nekoliko ordinala se označava ovako:
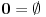
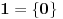
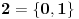
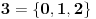
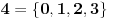
Tako ćemo iscrpeti sve konačne ordinale. Prvi sledeći se najčešće obeležava sa
i predstavlja skup svih konačnih ordinala, odnosno
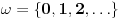
. To je najmanji ordinal kardinalnosti
, ali ima ih još. Sledeći je
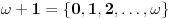
, pa zatim
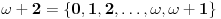
i tako dalje, i svi su oni prebrojivi, tj. kardinalnosti
. Neki ordinal naziva se početni ili inicijalni (nisam siguran da li se baš ovako kaže na srpskom jeziku) ako svi ordinali manji od njega imaju i manju kardinalnost. Znači, od do sada nabrojanih inicijalni su svi konačni i
. Sledeći inicijalni je
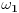
, što je zapravo skup svih konačnih i prebrojivih ordinala (tj.
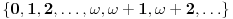
, i on ima kardinalnost
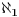
. Njegov sledbenik je, naravno,
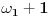
, pa zatim
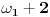
i tako dalje. Sledeći skok je do
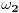
što je zapravo skup svih ordinala koji su bilo konačni, kardinalnosti
, ili kardinalnosti
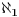
. Tako možemo da se igramo dokle hoćemo, pa kad sve to završimo onda ćemo naleteti na
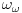
što je skup svih konačnih ordinala i onih kardinalnosti
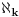
za ma koji nenegativan ceo broj
, i da ne nastavljam dalje jer je možda i ovo više nego što nam treba. Bitno je upamtiti da svaki možemo predstaviti kao uniju svih manjih od njega (što je jednom prilikom i rečeno u dokazu).
Nekoliko puta sam pomenuo da je jedan ordinal manji od drugog bez objašnjenja šta to znači jer smatram da je intuitivno jasno. Ipak, napisaću preciznije, potpunosti radi.
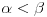
akko
ima isti tip uređenja kao neki početan podskup od
. Svaka dva ordinala su ili jednaka ili je jedan manji od drugog (tj. skup svih ordinala je totalno uređen). Osim toga, definišu se i operacije nad ordinalima kao što su sabiranje, množenje, stepenovanje, ali to već nije tema ovde. Ipak, ako želiš da kažem nešto više i o tome rado ću objasniti.
I za kraj, ne mogu da ostavim primer ordinala kardinalnosti
(pa ni najmanji takav ordinal) jer se još uvek ne zna gde zapravo
spada u gore navedenom spisku. Hipoteza kontinuuma kaže da je
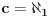
, ali to je nemoguće ni dokazati ni opovrgnuti, a matematičari nikako da se dogovore da li da je prihvate kao takvu ili da prihvate njenu negaciju. No, to što ne znamo kako izgleda nas ne sprečava da koristimo postojanje u zadacima, kao što sam i ja uradio.
[Ovu poruku je menjao Bojan Basic dana 04.01.2006. u 01:59 GMT+1]
Ljubičice crvena, što si plava kô zelena trava.
[Zadatak]: Pokrivanje prostora kružnicama
Registrovani: 2 ( Nedeljko, Ivan Dimkovic )
