• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 09.03.2002. Program sa vektorima. Again:) 12.09.2002. matematika 21.01.2004. Zadatak sa opstinskog takmicenja 04.01.2007. ArtCam radovi na net-u ? 28.02.2005. Jedan zadatak sa olimpijade 30.04.2005. Mturski rad-Poliedri(prizma/piramida/zarubljena p.. 22.06.2005. Elektrotehnika. Problem sa obrtnim vektorima!? 22.11.2005. Lep zadatak ....... 02.12.2009. ...zadatak...pascal... Navigacija Brisanje liste Aktuelne teme u ovom forumu: Geometrijski zadaci i trigonometrija Trigonometrijski problem Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

Bojan Basic Novi Sad SuperModerator Član broj: 6578 Poruke: 3996 *.adsl.sezampro.yu. Jabber: bojan_basic@elitesecurity.org ICQ: 305820253 +621 Profil [Zadatak]: Poliedri sa vektorima 03.12.2005. u 19:49 - pre 237 meseci Rešenje ovog zadatka zauzima dve rečenice i jedno je od najoriginalnijih (i najneobičnijih) rešenja koje sam ja ikada video. Iako formulacija izgleda komplikovano, rešenje je izuzetno jednostavno. Mislim i da je zadatak dosta poznat, ali nema veze. Svakoj strani poliedra pridružimo vektor normalan na nju usmeren ka spoljašnjosti intenziteta jednakog površini te strane. Dokazati da je rezultanta ovih vektora jednaka nuli. Ljubičice crvena, što si plava kô zelena trava. Odgovor na temu

uranium Beograd Član broj: 60097 Poruke: 543 *.eunet.yu. Jabber: uranium@elitesecurity.org ICQ: 324386953 +5 Profil Re: [Zadatak]: Poliedri sa vektorima 03.12.2005. u 21:17 - pre 237 meseci Za tetraedar tvrđenje zaista važi: Neka je proizvoljan tetraedar, onda je: . Tvrđenje će važiti i za svaki poliedar koji se može dobiti uzastopnim "lepljenjem" tetraedara po nekim njihovim podudarnim stranama, jer su vektori pridruženi tim stranama istog intenziteta, kolinearni, ali suprotnog smera. E sad, izgleda da se ne može svaki poliedar razbiti na tetraedre: In 1900, Dehn proved that not every prism can be dissected into a tetrahedron (Lenhard 1962, Ball and Coxeter 1987). Dakle, moguće je da je postavka pomalo neprecizna... ili je ovaj metod ograničenog dometa (što je i verovatnije )... Anyway, it's the end of the road for me [Ovu poruku je menjao uranium dana 03.12.2005. u 22:21 GMT+1] Attempt all the problems. Those you can do, don't do. Do the ones you cannot. Odgovor na temu

uranium Beograd Član broj: 60097 Poruke: 543 *.eunet.yu. Jabber: uranium@elitesecurity.org ICQ: 324386953 +5 Profil Re: [Zadatak]: Poliedri sa vektorima 03.12.2005. u 21:34 - pre 237 meseci U stvari,malo sam požurio Mislim da ovaj metod lepljenja ima malih problema. Davno sam čitao u nekoj Klarkovoj knjizi, navodno istinit slučaj sa nekog testa inteligencije gde se postavlja pitanje: koliko će imati strana telo koje nastaje lepljenjem po podudarnoj strani, pravilnog tetraedra i pravilne četvorostrane piramide... Dakle, obrazloženje koje sam dao u slučaju lepljenja, nije kompletno... ali je metod ipak korektan [Ovu poruku je menjao uranium dana 03.12.2005. u 22:39 GMT+1] Attempt all the problems. Those you can do, don't do. Do the ones you cannot. Odgovor na temu

Bojan Basic Novi Sad SuperModerator Član broj: 6578 Poruke: 3996 *.adsl.sezampro.yu. Jabber: bojan_basic@elitesecurity.org ICQ: 305820253 +621 Profil Re: [Zadatak]: Poliedri sa vektorima 03.12.2005. u 21:47 - pre 237 meseci Citat: uranium: Dakle, moguće je da je postavka pomalo neprecizna... ili je ovaj metod ograničenog dometa (što je i verovatnije :) )... Postavka je korektna, a zaista mi se čini da je metod ograničenog dometa. U svakom slučaju, i jedan deo je više od ničega. Citat: uranium: Dakle, obrazloženje koje sam dao u slučaju lepljenja, nije kompletno... ali je metod ipak korektan :) Nisam siguran šta ovim hoćeš da kažeš. Svakako da tvoj dokaz korektno rešava problem ukoliko razmatramo samo one poliedre koji se mogu dobiti lepljenjem tetraedara. Ljubičice crvena, što si plava kô zelena trava. Odgovor na temu

uranium Beograd Član broj: 60097 Poruke: 543 *.eunet.yu. Jabber: uranium@elitesecurity.org ICQ: 324386953 +5 Profil Re: [Zadatak]: Poliedri sa vektorima 03.12.2005. u 21:53 - pre 237 meseci Ako označimo sa i brojeve strana poliedara i , onda poliedar dobijen njihovim lepljenjem po podudarnoj strani ne mora imati strana Attempt all the problems. Those you can do, don't do. Do the ones you cannot. Odgovor na temu

Bojan Basic Novi Sad SuperModerator Član broj: 6578 Poruke: 3996 *.smin.sezampro.yu. Jabber: bojan_basic@elitesecurity.org ICQ: 305820253 +621 Profil Re: [Zadatak]: Poliedri sa vektorima 03.12.2005. u 22:16 - pre 237 meseci Slažem se, ali ne vidim kakve to ima veze. Ukoliko bi se svaki poliedar mogao razložiti na tetraedre onda bi tvoj dokaz bio kompletan. Međutim, to nije tačno i ispostavlja se da si rešio samo specijalan slučaj. Gde se tu pominje broj strana? Ljubičice crvena, što si plava kô zelena trava. Odgovor na temu

uranium Beograd Član broj: 60097 Poruke: 543 *.eunet.yu. Jabber: uranium@elitesecurity.org ICQ: 324386953 +5 Profil Re: [Zadatak]: Poliedri sa vektorima 03.12.2005. u 22:56 - pre 237 meseci E, onda se valjda razumemo Ja sam samo napisao da nisam obrazložio sve detalje u slučaju da se posle lepljenja desi da neke 2 strane polaznih poliedara postanu jedna strana (npr. spoje se po jednoj ivici, a leže u istoj ravni). U slučaju kada se to ne desi ja sam imao na umu da se dešava sledeće: Neka su postojećem poliedru pridruženi vektori a tetraedru koga dodajemo, vektori . Neka se lepljenje događa na stranama kojima su pridruženi vektori i . Vektori su označeni tako da bude: i . Dakle, važi: . Pa, će dobijeni poliedar imati pridružene vektore: . Pa iz i sledi tvrđenje, i tu zaista mislim da je sve korektno. A ako se desi onaj slučaj, trebalo je da pojasnim da će 2 pridružena vektora u zbiru dati baš vektor pridružen novonastaloj strani (kolinearni su, a površina je aditivna...) Onima koji su odmah imali u vidu i ovaj poslednji slučaj, se izvinjavam ako sam nepotrebno davio sa detaljima (ja sam naprosto to prevideo u prvi mah). Attempt all the problems. Those you can do, don't do. Do the ones you cannot. Odgovor na temu

Bojan Basic Novi Sad SuperModerator Član broj: 6578 Poruke: 3996 *.adsl.sezampro.yu. Jabber: bojan_basic@elitesecurity.org ICQ: 305820253 +621 Profil Re: [Zadatak]: Poliedri sa vektorima 03.12.2005. u 23:05 - pre 237 meseci Citat: uranium: A ako se desi onaj slučaj, trebalo je da pojasnim da će 2 pridružena vektora u zbiru dati baš vektor pridružen novonastaloj strani (kolinearni su, a površina je aditivna...) Aha, sad shvatam. Nisam odmah razumeo da želiš to da naglasiš jer mi se činilo da je to jasno, ali sad su dileme u svakom slučaju razjašnjene. Citat: uranium: Onima koji su odmah imali u vidu i ovaj poslednji slučaj, se izvinjavam ako sam nepotrebno davio sa detaljima (ja sam naprosto to prevideo u prvi mah). Ma nema potrebe da se izvinjavaš, bolje je napisati koji detalj više nego manje, ja jednostavno nisam odmah razumeo da želiš da na to skreneš pažnju i to je sve. Ljubičice crvena, što si plava kô zelena trava. Odgovor na temu

Farenhajt Goran Kapetanović Beograd Član broj: 78132 Poruke: 449 62.193.129.* +6 Profil Re: [Zadatak]: Poliedri sa vektorima 19.12.2005. u 11:38 - pre 236 meseci Hmmm... Ja ću malo da "kreiram", a onda neka neko to sroči strogo i/ili sažeto. 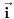Ako zamisliš da je poliedar sačinjen samo od letvica, sa šupljim stranama, i ako ga postaviš na neku ravan, pa ga pod bilo kakvim uglom osvetliš paralelnim snopom svetlosti, koji uvek možeš opisati nekim jediničnim vektorom , usmerenim od izvora ka poliedru - uz uslov da taj snop ne sme biti paralelan s projekcionom ravni - onda ćeš kao projekciju na toj ravni dobiti neki poligon, sačinjen od projekcija pojedinih strana poliedra. 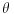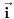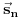Pošto je ugao između vektora i vektora površine određene strane poliedra jednak uglu između te strane poliedra i projekcione ravni, površina projekcije strane dobiće se kao . 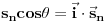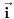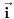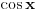Odatle sledi da ćemo, ako sumiramo te skalarne proizvode po "osvetljenim" stranama poliedra (dakle, po onima čiji vektori površine zaklapaju najmanje prav ugao s vektorom ), a zatim skalarne proizvode po "osenčenim" stranama poliedra (dakle, po onima čiji vektori površine zaklapaju najviše prav ugao s vektorom ), dobiti dva iznosa različitog znaka (zbog znaka funkcije ) ali iste apsolutne vrednosti, koja je jednaka površini projekcije poliedra na ravan. 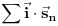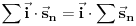Stoga je po CELOM poliedru jednaka nuli, a kako je , sledi da je . 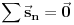[Ovu poruku je menjao Farenhajt dana 20.12.2005. u 18:09 GMT+1] Odgovor na temu

Bojan Basic Novi Sad SuperModerator Član broj: 6578 Poruke: 3996 *.smin.sezampro.yu. Jabber: bojan_basic@elitesecurity.org ICQ: 305820253 +621 Profil Re: [Zadatak]: Poliedri sa vektorima 19.12.2005. u 14:07 - pre 236 meseci Svaka čast! To nije ono što sam ja imao u vidu, ali i ovo rešenje mi se zaista sviđa. Evo totalno drugačijeg, fizičkog pristupa. Zamislimo da je poliedar iznutra šupalj (kao, recimo, fudbalska lopta) i upumpajmo vazduh u njega. U stanju ravnoteže vektori koji su opisani su upravo sile pritiska vazduha na strane, i njihova rezultanta je očigledno nula jer se radi o stanju ravnoteže. Ljubičice crvena, što si plava kô zelena trava. Odgovor na temu

Farenhajt Goran Kapetanović Beograd Član broj: 78132 Poruke: 449 62.193.129.* +6 Profil Re: [Zadatak]: Poliedri sa vektorima 19.12.2005. u 15:33 - pre 236 meseci Odlično! A elektroinženjeri bi rekli "fluks vektora jačine svakog homogenog polja kroz bilo kakvu zatvorenu površ jednak je nuli" (na šta se praktično svodi moj dokaz) i prešli na sledeći zadatak :) [Ovu poruku je menjao Farenhajt dana 19.12.2005. u 16:34 GMT+1] Odgovor na temu

zzzz milan kecman bluka Član broj: 11810 Poruke: 2164 *.dialup.blic.net. +197 Profil Re: [Zadatak]: Poliedri sa vektorima 19.12.2005. u 23:58 - pre 236 meseci Citat: Bojan Basic:  Evo totalno drugačijeg, fizičkog pristupa. Zamislimo da je poliedar iznutra šupalj (kao, recimo, fudbalska lopta) i upumpajmo vazduh u njega. U stanju ravnoteže vektori koji su opisani su upravo sile pritiska vazduha na strane, i njihova rezultanta je očigledno nula jer se radi o stanju ravnoteže. Dokaz (u hidrostatici) da je pritisak u tekućini skalar,a ne vektor je gotovo onakav kako je uradio Farenhajt A ovo \cdot;\dot;\cdots....Klikni na formulu pa vidi kako je napisano! [Ovu poruku je menjao zzzz dana 1.1.2006. u 01:05 GMT+1] [Ovu poruku je menjao zzzz dana 20.12.2005. u 01:07 GMT+1] ________________________________ Najbolja kritika formule za Sagnac effect: https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500 OK evo prave formule:P=2wft^2 [period] Odgovor na temu

Farenhajt Goran Kapetanović Beograd Član broj: 78132 Poruke: 449 62.193.129.* +6 Profil Re: [Zadatak]: Poliedri sa vektorima 20.12.2005. u 01:25 - pre 236 meseci Hvala na pomoći, zzzz! :)) Editovao sam svoju poruku. A moram da ispravim i grešku koju niko nije zapazio - ali koja neće uticati na tačnost dokaza: Naime, ugao između vektora površine i jediničnog vektora biće jednak uglu između strane poliedra i projekcione ravni samo ako je vektor normalan na projekcionu ravan. Uz, dakle, ograničenje da snop svetlosti mora biti normalan na projekcionu ravan, dokaz ostaje isti. [Ovu poruku je menjao Farenhajt dana 20.12.2005. u 04:57 GMT+1] Odgovor na temu

Bojan Basic Novi Sad SuperModerator Član broj: 6578 Poruke: 3996 *.smin.sezampro.yu. Jabber: bojan_basic@elitesecurity.org ICQ: 305820253 +621 Profil Re: [Zadatak]: Poliedri sa vektorima 20.12.2005. u 12:03 - pre 236 meseci Citat: zzzz: Dokaz (u hidrostatici) da je pritisak u tekućini skalar,a ne vektor je gotovo onakav kako je uradio Farenhajt Slažem se, ali verujem da velik broj ljudi zna za tu činjenicu ali ne zna dokaz, i stoga smatram da je OK pozvati se na to ne zadirući mnogo u pozadinu svega. Ljubičice crvena, što si plava kô zelena trava. Odgovor na temu

Farenhajt Goran Kapetanović Beograd Član broj: 78132 Poruke: 449 62.193.129.* +6 Profil Re: [Zadatak]: Poliedri sa vektorima 20.12.2005. u 14:10 - pre 236 meseci I mora se dodati još jedna napomena (koju će neki možda okarakterisati i kao cepidlačenje ili preteranu strogost): Iz činjenice da je ne može se pravolinijski zaključiti da je , već samo da je ta suma normalna na . Međutim, kako se bira proizvoljno, sledi da je normalna na svaki proizvoljno odabran vektor. E, sada možemo tvrditi da je . Odgovor na temu