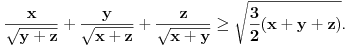Ne znam zašto se nigde ne pominje svođenje dokazivanja konveksnosti funkcija više promenljivih na slučaj jedne promenljive, pa hajde ja da napišem.
Neka je funkcija
definisana na konveksnom domenu. Tada je funkcija
(strogo) konveksna (odnosno konkavna) akko je za ma koje različite tačke
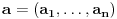
i
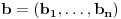
funkcija
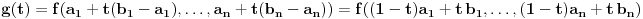
za
.
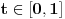
Tada se u slučaju diferencijabilnosti, odnosno dvostruke diferencijabilnosti može koristiti kriterijum za funkcije jedne promenljive, s tim da se to mora dokazati za sve međusobno različite
i
iz domena. Ukoliko je funkcija
definisana preko neke funkcije jedne promenljive kao u navedenom zadatku, onda se lako rešava onako kako je Sonec napisao.
Za funkcije jedne promenljive važi da je funkcija
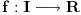
, gde je
pravi interval (ograničen ili neograničen) (strogo) konveksna akko je zadovoljen bilo koji od sledećih ekvivalentnih uslova:
1) Za ma koje
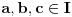
takve da je
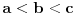
važi da je determinanta
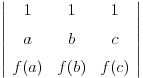
(strogo) veća od nule. Ovde "veća" bez "strogo" znači "veća ili jednaka".
2) Pod uslovom da je
najmanja vrednost intervala
, funkcija
je (strogo) konveksna na intervalu
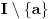
, važi da je
.
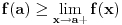
3) Pod uslovom je
najveća vrednost intervala
, funkcija
je (strogo) konveksna na intervalu
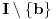
, važi da je
.
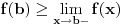
4) Ako za barem jedno
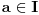
važi da je funkcija
,
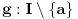
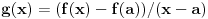
(strogo) monotono neopadajuća. Ovde "strogo monotono neopadajuća" znači "strogo rastuća".
5) Ako za svako
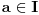
važi da je funkcija
,
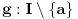
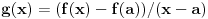
(strogo) monotono neopadajuća.
6) Pod uslovom da interval
nema najmanju niti najveću vrednost i da je funkcija
diferencijabilna na njemu, važi da je funkcija
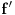
monotono neopadajuća, i da u slučaju da se traži stroga konveksnost važi da
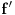
nije konstantno ni na jednom pravom intervalu.
7) Pod uslovom da interval
nema najmanju niti najveću vrednost i da je funkcija
dva puta diferencijabilna na njemu, važi da je funkcija
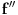
nenegativna, i da u slučaju da se traži stroga konveksnost važi da
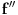
nije konstantno jednako nuli ni na jednom pravom intervalu.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Jedna nejednakost
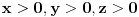, dokazati da je:
Registrovani: 0 ( 0 )
