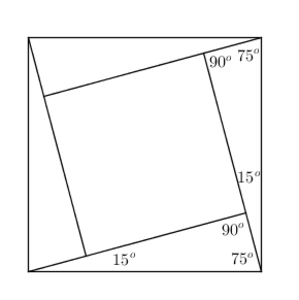
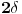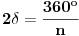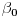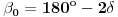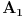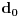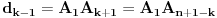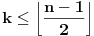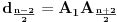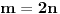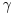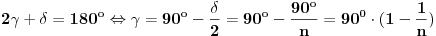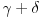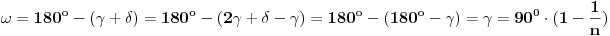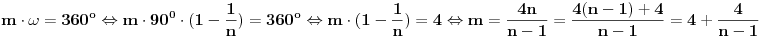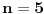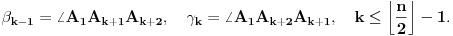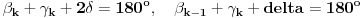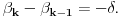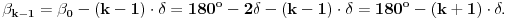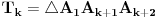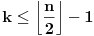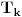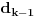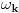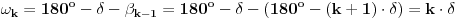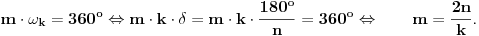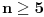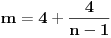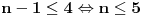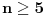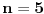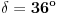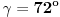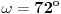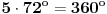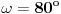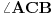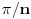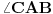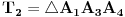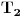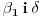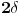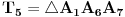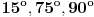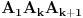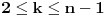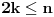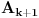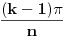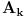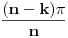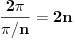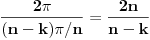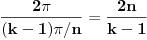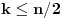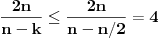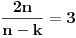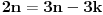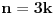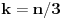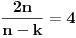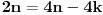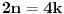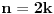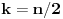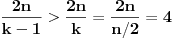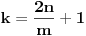3.) Pošto treći deo zadatka nije precizno formulisan, predlažem rešenje zasnovano na pretpostavci da je treća figura na slici u uvodnoj poruci dvodimenzionalna figura, prsten određen sa dva pravilna mnogougla. Možda je moguće od dijagonalnih trouglova pravilnog mnogougla sastaviti i telo koje podseća na torus ( torus je trodimenzionalno telo ), ali bi takva varijanta zadatka bila teža, samim tim i „rekonstrukcija“ zadatka, ako nije precizno formulisan, bila teža.
Ako spojimo dva susedna temena pravilnog
n-tougla sa središtem kružnice opisane oko tog
n-tougla dobijamo karakteristični trougao tog pravilnog
n-tougla. Ugao naspram osnovice
a tog jednakokrakog trougla, odnosno centralni ugao opisane kružnice nazovimo centralnim uglom pravilnog
n-tougla i obeležimo sa
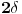
, pa je
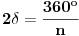
. Unutrašnji ugao
n-tougla obeležimo sa
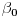
. Mera tog ugla je
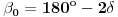
. Pošto su ti uglovi suplementni sledi da je spoljašnji ugao pravilnog
n-tougla jednak centralnom uglu tog pravilnog
n-tougla.
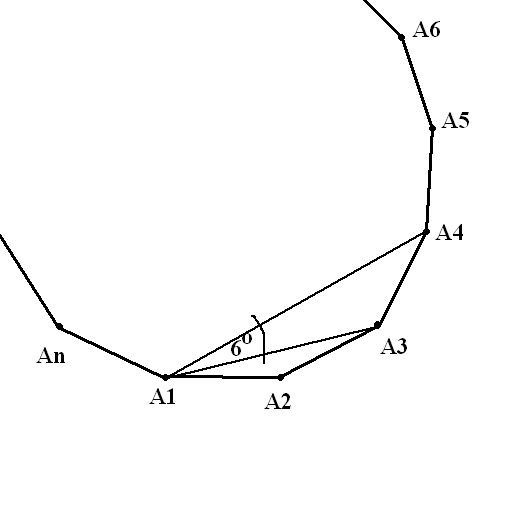
Konstruišimo sve dijagonale koje sadrže teme
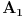
(ima ih ukupno
n-3), a onda konstruišimo i osu simetrije pravilnog
n-tougla kroz tačku
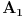
. Ako je
n neparan broj, broj dijagonala je paran i svaka dijagonala ima tačno jednu osno simetričnu dakle podudarnu dijagonalu. Ako je
n paran broj, broj dijagonala je neparan, pa osim parova simetričnih dijagonala postoji jedna koja leži na osi simetrije i ona nema simetričnu dijagonalu. To je najduža dijagonala koja je jednaka prečniku opisane kružnice. Stranicu
a, zbog formula koje ćemo koristiti, obeležimo i sa
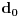
. Dijagonale obeležimo sa
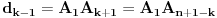
gde je prirodan broj
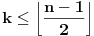
. Ako je
n paran broj, imamo i najdužu dijagonalu
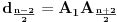
.
Ovim dijagonalama je pravilan
n-tougao podeljen na
n-2 trougla, koji kod temena
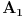
imaju ugao sa merom

( Miki je to objasnio). Zbog podudarnosti simetričnih trouglova, prilikom rešavanja zadatka razmotrimo samo „polovinu“ trouglova.
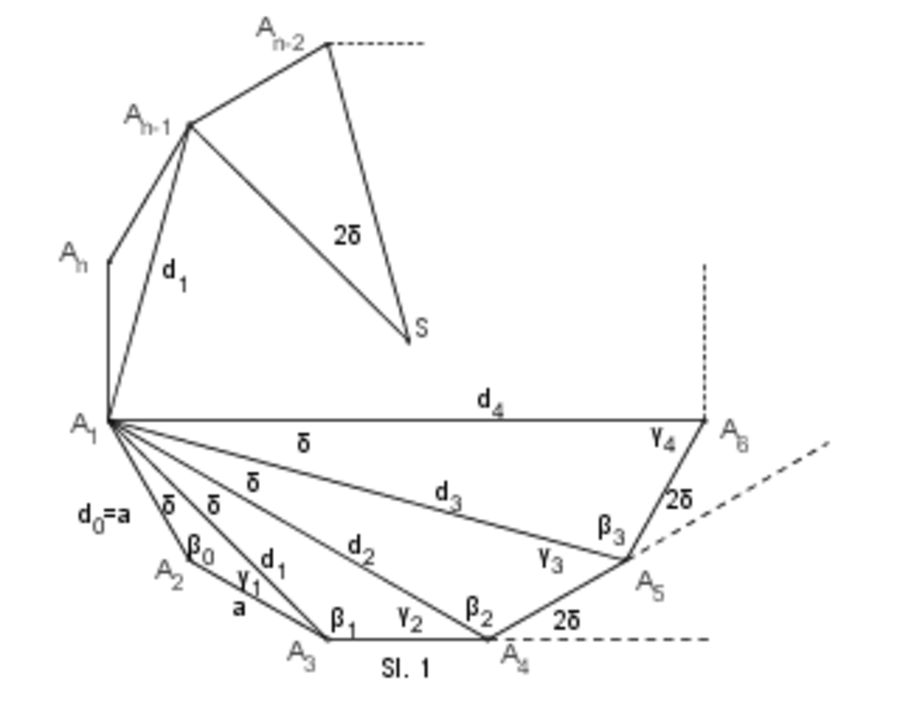
Neka je broj temena
n, neparan broj. Uočimo trougao određen sa dve najduže, jednake dijagonale.
Ako od trouglova podudarnih sa uočenim trouglom, „pravimo“ pravilan
m-tougao, tako da temena naspram osnovica tih jednakokrakih trouglova budu u jednoj tački, a susedni trouglovi imaju zajednički krak, centralni ugao tog
m-tougla će biti ugao

, ugao koji je polovina centralnog ugla pravilnog
n-tougla. Prema tome, da bi ti centralni uglovi formirali pun ugao, odnosno da bi od tih trouglova satavili pravilan m-tougao, treba da ih bude dva puta više nego što je centralnih uglova u pravilnom
n-touglu, odnosno mora da bude
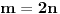
.
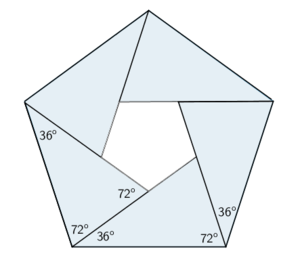
Proverićemo da li je od tih trouglova moguće „napraviti“ treću, nekonveksnu figuru sa slike iz uvodnog posta. Nazovimo tu figuru pravilan mnogougaoni prsten.
Ugao naspram osnovice tog trougla ima meru

. Ugao na osnovici obeležimo sa
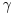
, pa je
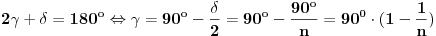
.
Ako je spoljašnja kontura pravilnog mnogougaonog prstena pravilan
m-tougao, ugao suplementan uglu
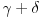
, obeležimo ga sa

, mora biti jednak centralnom uglu tog pravilnog
m-tougla.
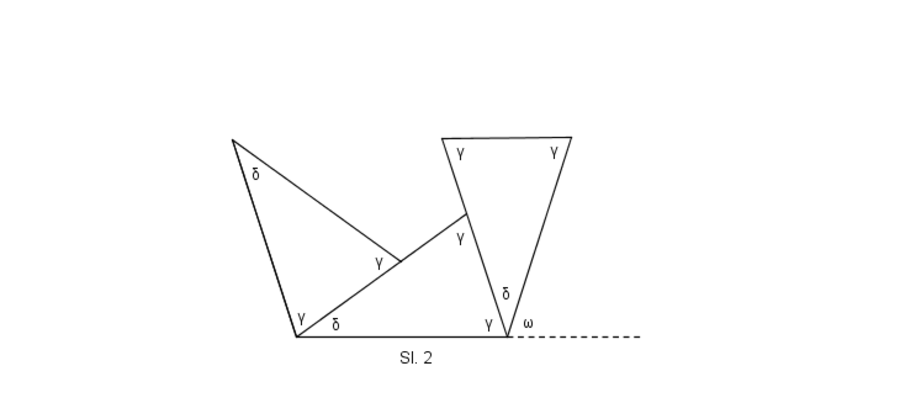
Odredimo taj centralni ugao, odnosno ugao

.
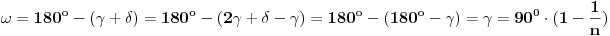
.
Ugao

može da bude centralni ugao pravilnog
m-tougla ako postoji prirodan broj
m, veći od 2, takav da je
m-tostruki umnožak tog centralnog ugla, jednak punom uglu:
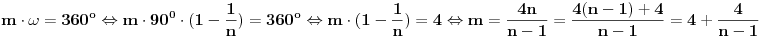
gde je
n neparan prirodan broj veći od 3. Iz poslednje jednakosti zaključujemo da će
m biti prirodan broj samo ako je
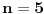
.
Prema tome od jednakokrakih toruglova određenih sa dve najduže susedne dijagonale u pravilnom n-touglu sa neparnim brojem temena, možemo formirati pravilan mnogougaoni prsten samo ako je n=5. Konture tog prstena su dva pravilna petougla.
Neka je sada
n prirodan broj veći od 3 (pošto trougao nema dijagonale).
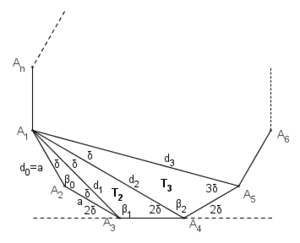
Označimo uglove trouglova određenih dijagonalama na sledeći način:
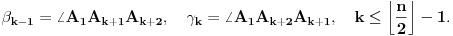
Za navedene uglove imamo relacije
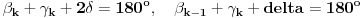
.
Ako oduzmemo ove jednakosti dobijamo relaciju
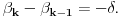
Prema tome ovaj niz uglova je aritmetički, pa je
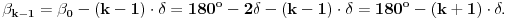
Definišimo niz trouglova određenih dijagonalama mnogougla
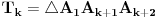
.
Pretpostavimo da za neki prirodan broj
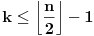
, od trouglova podudarnih sa trouglom
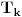
, definisanim u pravilnom n-touglu, možemo formirati pravilan mnogougaoni prsten, sa
m temena na spoljašnjoj konturi.
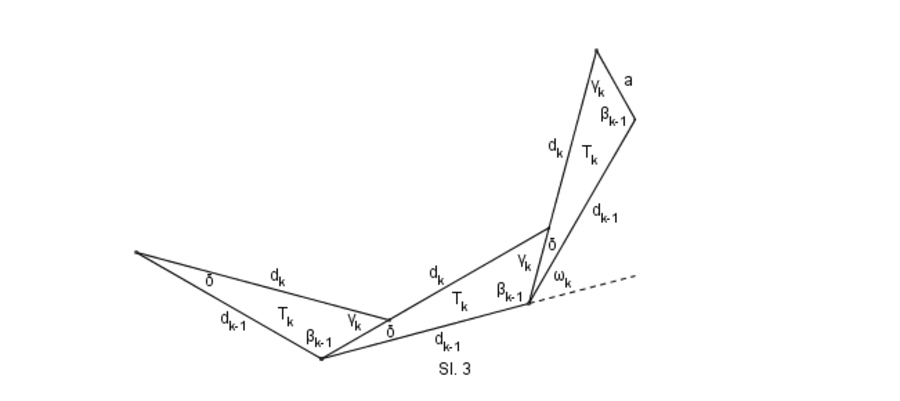
Spoljašnji ugao spoljašnje konture prstena - pravilnog m-tougla sa stranicom
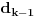
obeležimo sa
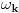
, a njegova mera je
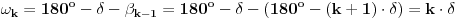
.
Pošto je taj spoljašnji ugao pravilnog m-tougla jednak centralnom uglu tog m-tougla, tačna je jednakost
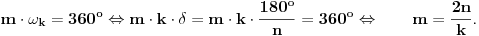
Prema tome, od trouglova podudarnih sa trouglom
Tk , definisanog u pravilnom n-touglu, možemo napraviti mnogougaoni prsten, samo ako je broj 2n deljiv sa k.
Pošto je trougao
T1 jednakokraki, slično kao što je urađeno za jednakokraki trougao, određen najdužim dijagonalama u pravilnom mnogouglu sa neparnim brojem stranica, možemo proveriti da od trouglova podudarnih sa trouglom
T1, možemo sastaviti pravilan mnogougao samo ako je broj temena datog mnogougla
4 ili
6.
[Ovu poruku je menjao jans dana 24.06.2025. u 22:37 GMT+1]
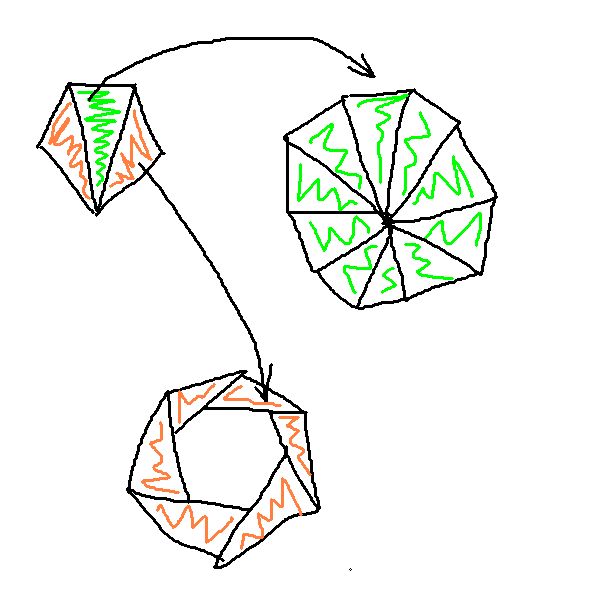




 Mnogougao i dijagonale
Mnogougao i dijagonale