[es] - Mnogougao i dijagonale

MajorFatal
Milija Jakic
opravljam oluke, 1337LAB
Bg

Član broj: 36595
Poruke: 1525
87.116.162.*

+615 Profil

^{03.06.2025. u 22:28 - pre 11 dana i 20h}

Postoji pravilan mnogougao A1, A2, A3 .. An-1, An. Ugao A3A1A4 iznosi 6 stepeni.

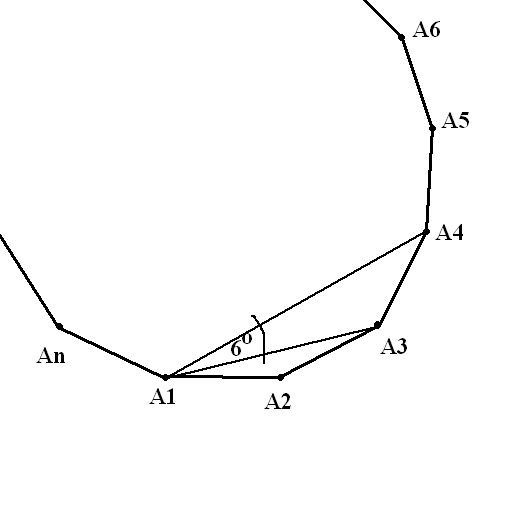
1.) Koliko takav mnogougao ima dijagonala?
2.) Koliki je zbir svih unutrašnjih i svih spoljašnjih uglova tog mnogougla?
3.) Ukoliko se povuku sve dijagonale iz jednog temena, i na taj način mnogougao podeli na trouglove, svaki takav trougao umnožen više puta može da posluži za formiranje svojevrsnog torusa, tako da se trouglovi nikad ne preklapaju. A ako je mnogougao sa neparnim brojem temena, te postoji centralni takav trougao, onda se ređanjem takvog umnoženog trougla, u krug dobija novi mnogougao, a da se trouglovi nikad ne preklope.

1.) Je međuopštinsko 1997 za 7 razred osnovne 2.) Sam ja izmislio 3.) Viđeno na internetu

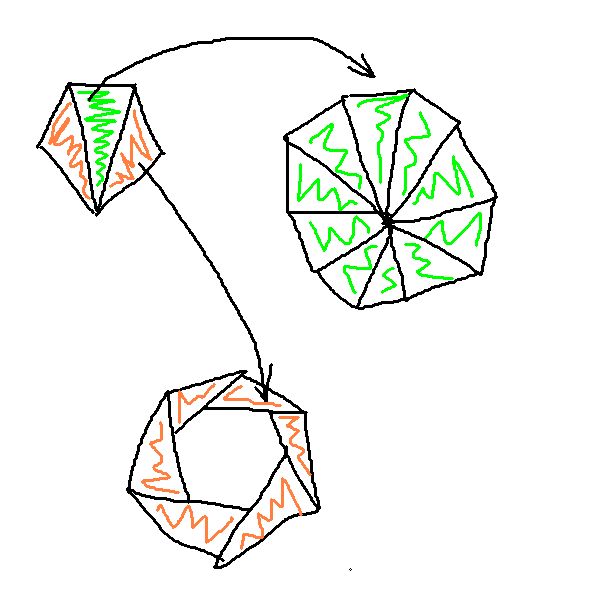
Ilustracija uz 3.)

Nemoj da pricas?

Prikačeni fajlovi

mnogougao.jpg - 43.92k

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2059
*.mbb.yettel.rs.

+401 Profil

Re: Mnogougao i dijagonale

^{08.06.2025. u 12:22 - pre 7 dana i 6h}

Centralni ugao A3-O-A14 je 11*360°/n. Periferijski A3-A1-A14 je pola od toga. Odatle se lako nađe da je n=330.

Prva dva dela su trivijalna.

Odgovor na temu

MajorFatal
Milija Jakic
opravljam oluke, 1337LAB
Bg

Član broj: 36595
Poruke: 1525
87.116.166.*

+615 Profil

Re: Mnogougao i dijagonale

^{08.06.2025. u 23:10 - pre 6 dana i 19h}

Nisam siguran da razumem ..

Citat:

miki069: Centralni ugao A3-O-A14 je 11*360°/n.

Ovo hajd u redu valjda ..

Citat:

Periferijski A3-A1-A14 je pola od toga. Odatle se lako nađe da je n=330.

Prva dva dela su trivijalna.

Ovo ne razumem. U knjizi je rešenje da je u pitanju mnogougao sa 30 stranica, i da takav ima 405 dijagonala. I fulao sam koje takmičenje je bilo u pitanju, okružno, a ne međuopštinsko ..

Ilustracija uz prvi zadatak, ugao A3-A1-A4 je 6 stepeni.

Nemoj da pricas?

Prikačeni fajlovi

mnogougao1.jpg - 13.33k

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2059
*.mbb.yettel.rs.

+401 Profil

Re: Mnogougao i dijagonale

^{08.06.2025. u 23:42 - pre 6 dana i 19h}

Majore pročitao sam teme A14 umesto A4.
Tako sam i računao.

Neka je O centar opisane kružnice oko mnogougla.
Centralni ugao A3-O-A4 je 360°/n.
Periferijski ugao, nad istim kružnim lukom, A3-A1-A4 je pola od toga.

Iz jednačine 1/2*(360°/n) = 6° se dobija da je n=30.

Iz svakog od 30 temena konstruišu se duži u ostalih 29 temena.
Ukupno 30*29=870 usmerenih duži (vektora).
Od toga su 30*2= 60 vektori stranica.
Ostaje 870-60=810 vektora dijagonala.
Pošto dijagonala nije vektor, nego duž, broj dijagonala je
1/2*810 = 405.

_{[Ovu poruku je menjao miki069 dana 09.06.2025. u 01:10 GMT+1]}

Odgovor na temu

MajorFatal
Milija Jakic
opravljam oluke, 1337LAB
Bg

Član broj: 36595
Poruke: 1525
87.116.166.*

+615 Profil

Re: Mnogougao i dijagonale

^{09.06.2025. u 00:10 - pre 6 dana i 18h}

Sve jasno, ja nisam umeo da rešim, a u knjizi je neko komplikovano rešenje gde su docrtavali duž A4-A2, a unutrašnji ugao mnogougla imenovali 2alfa itd .. ti si rešio mnogo jednostavnije. Svaka čast!

Nemoj da pricas?

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2059
77.46.139.*

+401 Profil

Re: Mnogougao i dijagonale

^{09.06.2025. u 12:49 - pre 6 dana i 6h}

2) Zbir svih unutrašnjih uglova je (30-2)*180 stepeni, a zbir svih spoljašmjih je 360 stepeni.

3) Nije mi baš sve jasno.

Odgovor na temu

MajorFatal
Milija Jakic
opravljam oluke, 1337LAB
Bg

Član broj: 36595
Poruke: 1525
*.dynamic.a1.rs.

+615 Profil

Re: Mnogougao i dijagonale

^{09.06.2025. u 18:01 - pre 6 dana i 1h}

Citat:

miki069: 2) Zbir svih unutrašnjih uglova je (30-2)*180 stepeni, a zbir svih spoljašmjih je 360 stepeni.

Jest, a pošto je 360 baš 2 x 180 mislio sam da se sve smandrlja u zbir svih unutrašnjih i spoljašnjih uvek: n x 180 :) Ne verujem da će koristiti u zadacima ..

Citat:

3) Nije mi baš sve jasno.

Ni meni, ako se n-tougao podeli dijagonalama iz jednog temena na troglove, uvek ih je moguće spakovati u torus, ili novi n-tougao ...

Nemoj da pricas?

Odgovor na temu