[es] - Da li je zakon poluge pogrešan

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.opera-mini.net.

+2801 Profil

^{18.12.2012. u 11:08 - pre 150 meseci}

Obzirom da vam neke stvari jesnostavno ne vredi objasnjavati jer nemate potrebne kognitivne sposobnosti, imam jedno prosto pitanje. Imate li ikakvu referencu za budalastinu "telo T se ne nalazi u sistemu S"?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{18.12.2012. u 23:55 - pre 150 meseci}

Ova skica što je učitao @atelago sasvim je dobra za razmatranje koriolisovog ubrzanja.

Gaspard-Gustavea Coriolisa i Jean-Victora Ponceleta u periodu od 1819–1839 opisivali su sile na
djelovima raznih mašina.Uočena pojava sile pri radijalnom kretanju rotirajuće mase navela ih je da uvedu nove pojmove u dinamiku.Živi rad,nakupljeni rad,energija i takve stvari.Do tad se koristio zakon o količini kretanja i održanju momenta.
Većina ljudi je iskusila da pri potezanju konopca kroz neki otvor,a ako se donji kraj vrti,osjeti neobičan porast otpora izvlačenju.Usput primjete da se kraj koji visi zavrtio mnogo brže.(Da ne pričamo o piruetama klizačica koje osjetimo samo vizuelno.)

Coriolis sasvim sigurno nije izvodio proračun te inercijalne sile na bazi zakona o održanju energije.Naprimjer da iz izraza za kinetičku energiju nađe izvod,pa da takav prirast izjednači sa diferencijalom uloženog rada centripetalne sile itd.Pa da onda ide provjeravati eksperimentalno da li mu teorija valja.Radio je obratno.
Pravljene su probe i bilježeni rezultati mjerenja.Od ranije je bio poznat način izračuna centrifugalne sile i Njutnv zakon o sili,masi i ubrzanju.Sad ćemo vidjeti šta su odmah mogli neobično uočiti na ovom @galetovoj spravi……..
-Ako se rotirajuća masa prevuče sa R na R/2 potezanjem konopca,obodna brzina se znatno poveća.
-Ugaona brzina još očiglednije.
-Centripetalna sila ,(potezanja konopca) takođe nekako naglo raste duž puta pomjeranja.
-Uticaj radijalne brzine na prethodne pojave se ne primjećuje.
Sad treba napraviti finija mjerenja da bi se uočile neke zakonitosti.Tako su radili oni.

(Ja ću te rezultate umjesto mjerenjem napraviti računski jer znam zakonitosti.Usput,prije nego nastavim, zna li neko kolika će centripetalna sila biti na R/2 ako je bila poznata na početku?)…....

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{19.12.2012. u 09:34 - pre 150 meseci}

Citat:

zzzz: Coriolis sasvim sigurno nije izvodio proračun te inercijalne sile na bazi zakona o održanju energije.Naprimjer da iz izraza za kinetičku energiju nađe izvod,pa da takav prirast izjednači sa diferencijalom uloženog rada centripetalne sile itd.Pa da onda ide provjeravati eksperimentalno da li mu teorija valja.Radio je obratno.

(Ja ću te rezultate umjesto mjerenjem napraviti računski jer znam zakonitosti.Usput,prije nego nastavim, zna li neko kolika će centripetalna sila biti na R/2 ako je bila poznata na početku?)…....

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{20.12.2012. u 18:20 - pre 150 meseci}

Citat:

zzzz:
(Ja ću te rezultate umjesto mjerenjem napraviti računski jer znam zakonitosti)…....

Pa porodi se, već, aman!

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{21.12.2012. u 00:30 - pre 150 meseci}

Donekle je Nedeljko u pravu sa onim podvlačenjem .Pokušavam doprijeti do originalnih papira gospodina Coriolisa.Nema ih direktno na internetu,a meni se ne plaća arhivska kopija.Da pravim svoje eksperimente za zakon o Corijolisovoj sili,nemam zasad vremena.Predložio bih Nedeljku da to obavi.

Dakle,umjesto da ganja muve koje krivudaju po sobi neka uzme komad čvrste špage dužine 2 metra.Na jedan kraj zavezati težak šaraf.Predvostručiti špagu tako da slobodni kraj i šaraf budu u desnoj ruci.Lijevom rukom odmaknuti presavijenu sredinu maksimalmo od sebe u horizontalnom smjeru.Ispustiti šaraf iz desne ruke da se njiše kao klatno,a drugi kraj zadržati.Nagnuti glavu malo više naprijed i desno da bi mogao osmotriti kad će klatno pri njihanju biti blizu najniže tačke.Tada traba desnom rukom što jače povući slobodni kraj kako bi se smanjio radius njihanja klatna.Ponoviti 3x i snimati video kamerom. Okačiti na YOU TUBE.To bi bio lijep dokaz Coriolis efekta.
Ako Nedeljko neće to da provjeri,a želi saradnju onda neka proba odgovoriti na: Zna li neko kolika će centripetalna sila biti na R/2 ako je bila poznata na početku?)…....(Početni uslovi su zadani:poznata masa,radijus rotacije i ugaona brzina,pa prema tome i dotična sila.)
Pomoć potražiti ovdje („Klasična mehanika“ od Zvonko Glumac na strani oko 280/(od636): http://www.fizika.unios.hr/~zglumac/utm.pdf

(Za @atelaga:Polako,ovo je ključna tačka zbog koje sam postavio ovu temu sa alatkom iz kamenog doba.Zaslužio je to gotovo zaboravljeni veliki genije gospodin Koriolis.)

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{22.12.2012. u 12:49 - pre 150 meseci}

Vratimo se na sliku koju je postavio @atelago.Početni uslovi su ovakvi:
Masa

rotira brzinom

na udaljenosti

od centra rotacije.Pri tom je centripetalna sila

,
kinetička energija

,a ugaona brzina

Ako bi povlačenjem konopca skraćivali radijus rotacije,desile bi se neke promjene.Coriolis je eksperimentalno ustanovio da se utrošeni rad na to povlačenje na neki način transformisao u dodatnu kinetičku energiju mase koja rotira.Od tada se zakon o održanju energije redovno primjenjuje u mehanici.Držimo se ovog zakona da vidimo šta će se povlačenjem konopca mijenjati.
Označimo sa

put mase ka centru tako da je trenutni radijus rotacije

.
Trenutna kinetička energija na tom r se može izraziti trenutnom obodnom brzinom v,a odatle i diferencijalni prirast energije.Taj prirast bi trebao biti jednak diferencijalnom radu što ga centripetalna sila pravi na diferencijalu puta.

,..

Izjednačavanjem dE i dA ,malo sredimo, pa dobijemo

Integracijom imamo

,
c je konstanta integracije koju izračunamo iz početnih uslova.

, pa je

,

Sada je lako iz ovoga odrediti ugaonu brzinu,centripetalnu silu i kinetičku energiju u ovisnosti o x.Tako izlazi da je za x=R/2 obodna brzina uvećana za 2 puta,ugaona brzina za 4 puta.Energija je veća za 4 puta,a centripetalna sila 8 puta.Integracijom se može izračunati rad centripetalne sile na tom putu.Izlazi upravo u skladu sa bilansom energije:

Sada ostaje da se razmotri šta je to povećalo intenzitet obodnoj brzini v.Mora da je neka sila.Izračunaćemo i nju,a ako treba i eksperimentalno izmjeriti.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{23.12.2012. u 10:21 - pre 150 meseci}

Koriolisova sila se može izračunati iz prethodno izvedenog zakona obodne brzine v=v(r).

, ovdje je brzina data u funkciji puta x i početne brzine v(0) na prečniku R.Radijus na kome se ostvaruje brzina v je

.Za izračunavanje obodne (Koriolisove) sile koja tangencijalno ubrzava masu,treba nam prvi izvod brzine po vremenu,tj obodna akceleracija.Potom ćemo uz pomoć drugog Njutnovog zakona izraziti silu.

,.............gdje je

,............w je brzina kretanja mase m ka centru rotacije.

**************************

,.........To je ta Koriolisova sila.
**************************
Račun je sasvim korektan.Skalarno je proveden radi pojednostavljenja i zgodnog izbora vektorskih veličina.Nema sumnje u ispravnost formule.
Potrražimo li na internetu ovu formulu nailazimo na :

,...Teško je naći kako je to izvedeno.
A to je posebna priča.I lijep "dokaz" da je zakon poluge pogrešan,a perpetummobile moguć.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{24.12.2012. u 15:09 - pre 150 meseci}

Odgovor na temu

bigkandor
Antispin Technologies

Član broj: 300656
Poruke: 252
*.yourproxyhost.com.

+228 Profil

Re: Da li je zakon poluge pogrešan

^{24.12.2012. u 15:24 - pre 150 meseci}

Da, da, da, lijep "dokaz". "Dokaz" a la Mister Spin. Odličan primer kako sve može da bude "matematički precizno" a logička posledica apsurdna. Jer da je zaista reč o "dokazu" znamo iz svakodnevnog iskustva budući da poluga "radi" a za perpetuum mobile ostaje samo mašta.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{24.12.2012. u 23:55 - pre 150 meseci}

Na redu je precizna provjera iznesenog računa.Zatim provjera istog računa u vektorskom obliku.
Pa onda analiza energetskog bilansa ako je zvanična i opšteprihvaćena verzija formule dobra.

-----------------
Ali prije toga mora se istjerati na čistac jedna stvar.Da li je Koriolisova sila stvarna ili fiktivna sila?Inače odosmo u vrtlog filozofije tipa @Nedeljko.

Zato, spustimo se na kratko na realno tlo i praktičan posao.Probajmo napraviti jednu spravu.Neka to bude masivan zamajac koji če na jednom djelu imati radijalno kliznu masu.Taj teg je iz dva dijela spojen vijcima radi montaže.
Ima masu 10 kg.Maksimalna brzina prema centru u jednom ciklusu je W=10m/s.Zamajac se vrti sa 3000 o/min.(Ubaciću sliku kao prilog.)

Izračunati presjek 4 vijka (crveno označena) koji pričvršćuju teg ako je dozvoljeno naprezanje 100 N/mm^2.(Zanemariti promjenu ugaone brzine zamajca.)

Mogući odgovori su eksperimentalno provjerljivi.Navedimo ih sve onako intuitivno:

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Prikačeni fajlovi

Koriolisov_zamajac.JPG - 12.86k

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{26.12.2012. u 23:33 - pre 150 meseci}

Pregledajući raznu literaturu imamo dva moguća odgovora.
(vlada neka čudna konfuzija.)

1-Koriolisova sila je fiktivna ili prividna.A taj privid se javlja kod složenih gibanja.Naprimjer djete na vrtešci baci loptu ka centru,a ona mu prividno odleti u stranu itd itd.Po ovome nema nikakve sile u vijcima,nema opasnosti da se pokidaju.
2-Koriolisova sila ima realan efekat,i spada u grupu inercijalnih.Nije baš prava,a računa se

, ..za naš slučaj to je

Iz nekih razloga meni se čini da je ova sila dvostruko manja (31400 N).Treba izanalizirati obe jednačine,kako su nastale i šta predstavljaju.Provjeriću energetsku bilansu za obe verzije.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{27.12.2012. u 23:37 - pre 150 meseci}

Evo te analize bazirane na zakon o održanju energije:
Rad centripetalne sile

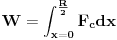
(engleski rad=Work).
Slika:

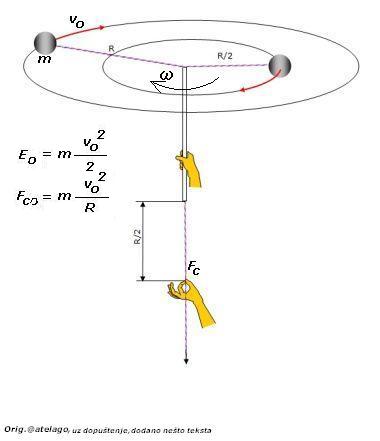
1)Najprije za slučaj kada je koriolisovo ubrzanje

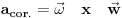
Ranije je već izračunato da je obodna brzina

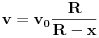
,a i centripetalna sila

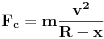
..uvrstimo to..

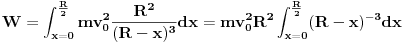
Rješimo integral,uvrstimo granice pa imamo

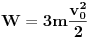
Ako znamo da je početna energija

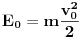
,a obodna brzina nakon puta x=R/2 naraste na dvostruku vrijednost,kinetička energija će iznositi

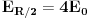
............... Vidimo da je

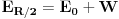
,zakon o održanju energije vrijedi.
---------------------
2)A sada za slučaj kada je koriolisovo ubrzanje

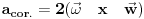
...a to je zvanični i „opšteprihvaćeni“ izraz.
Obodna brzina će zbog dvostruko većeg ubrzanja dvostruko brže rasti.Vrijeme se može izvući iz radijalne brzine w i puta x=R/2.Neću ovdje raspisivati formule takvog diferencijalnog računa, a ko želi (i zna taj račun) može provjeriti ovo:Brzina na kraju će biti trostruka,a kinetička energija devetostruka.Utrošeni rad zbog potezanja konopca,tj rad centripetalne sile je 27/4 početne
energije.Zajedno to je 31/4 početne.Preostaje do 36/4,da se zaradilo:

.
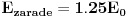
Ovo je divan „dokaz“ za mogućnost pravljenja Per-moB.Krasna stvar,samo da li je istinita?

Ali ako ne vjerujete u takve mašine nemojte odmah navaliti spaljivati sve knjige u kojima za Koriolisovo ubrzanje ugledate ono 2 ispred omege.Radije hajmo zajedno napraviti još dva koraka.

-1)Napravimo plan što jednostavnijeg eksperimenta i izvedimo ga.
-2)Ako eksperiment pokaže da ona dvojka ne treba onda pronađimo u teoretskim vodama gdje je napravljena fatalna greška.

Ove dvije stavke je lako odraditi što će i biti predmet mojih sledećih javljanja.Ali za početak i lagano razumjevanje moram uvesti jedan pojam:“Ajnštajnovi Sljedbenici“,skraćeno „AS“.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Prikačeni fajlovi

Atelago_cor..JPG - 14.1k

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{28.12.2012. u 14:01 - pre 150 meseci}

Ovo je ipak malo komplikovano. Evo, zato, jednostavnijeg primera:

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{28.12.2012. u 22:49 - pre 150 meseci}

Caka je u tome što ne znaš da računaš kinetičku energiju.

nije

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

bigkandor
Antispin Technologies

Član broj: 300656
Poruke: 252
*.yourproxyhost.com.

+228 Profil

Re: Da li je zakon poluge pogrešan

^{28.12.2012. u 22:54 - pre 150 meseci}

Atelago, aj sve ponovo izračunaj ali uzmi u obzir da se masa rakete smanjila za masu goriva utrošenog za potisak.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{28.12.2012. u 23:16 - pre 150 meseci}

Kao što je pokazano, zvanična „opšteprihvaćena“ formula za Koriolisovo ubrzanje ne drži vodu ako se testira zakonom o održanju energije.Ogromno odstupanje bi trebalo da se može eksperimentalno provjeriti.Probajmo organizovati ovako nešto:
-Napravimo klatno sa masom m na užetu dužine R.Ako se pusti sa visine R imaće maksimalnu brzinu u najnižem položaju,i to približno

..Pokušajmo za to vrijeme dok je klatno približno u najnižoj tački povlačenjem skratiti mu radijus rotacije na pola.Ovo radijalno kretanje inducira Koriolisovu silu pa se masa dodatno ubrzava.Na dvostruku ili trostruku vrijednost pitanje je sad.
Napravimo prepreku u koju će udariti masa zamajca nakon što nastavi kretanje.Neka bude na visini polaska kuglice da bi eliminisali potencijalnu energiju visine .
Napravimo slobodan pad kuglice iste mase na tu istu prepreku.Mjenjajmo visinu sve dok efekad udara ne bude što sličniji klatnu.Izračunajmo brzinu iz poznate visine.Uzmimo u obzir da je osim rada centripetalne sile uložen i rad gravitacione sile,ali i početna energija eliminisana.Kuglica na klatnu trebala bi imati kinetičku energiju jednaku 8.5mgR ,a ona koja pada mgH.Odatle H=8,5R.
Za dvostruko manje Koriolisovo ubrzanje (koje drži vodu),sličnim računom H=3.5R.Probajmo!
Slika-

@atelago,ajde pogledaj: http://www.elitesecurity.org/p2721273

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Prikačeni fajlovi

Eksperiment_Coriolis_J.JPG - 49.81k

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{29.12.2012. u 05:33 - pre 150 meseci}

Citat:

Nedeljko: Caka je u tome što ne znaš da računaš kinetičku energiju.

nije

Caka je u tome što je tebi važno da budeš uvek saboter i da smetaš. Ko je računao ΔE_k?
Ako ti je lakše da shvatiš onda zamisli da sam računao kinetičke energije dveju raketa od
kojih jedna ima duplo veću brzinu od druge. Računao sam odnose njihovih energija a ne ΔE_k
(ukoliko uopšte praviš razliku šta je odnos energija a šta prirast energije. Uvek praviš svoje
izmišljotine koje pripisuješ drugom pa onda odgovaraš sam sebi).

Citat:

bigkandor: Atelago, aj sve ponovo izračunaj ali uzmi u obzir da se masa rakete smanjila za masu goriva utrošenog za potisak.

Ja ne bih tako! To otežava stvar. Radije ću se opredeliti za drukčiji pogon raketa.
Jasnije će biti ako raketama damo ubrzanje pomoću nekih polja sila u referentnom
sistemu koja se uključuju i isključuju po našoj volji i na mestima gde mi želimo i koliko
želimo. U tom slučaju mase raketa se ne menjaju.
Naravno, i tu ima problema, ali zamislimo da je to moguće ostvariti u principu.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{29.12.2012. u 08:34 - pre 150 meseci}

@atelago:Ko ima bolji perpetuum mobile?
Šta ovdje ne valja?U čemu je caka?
Recimo da znaš u čemu je caka,ali ipak ću te uvrstiti na popis AS zbog pretjeranih pozivanja na inercijalne sisteme.A o tome ću napisati sledeću poruku u kojoj se jasno objašnjava kako je došlo do krivog izvođenja formule za Koriolisovu silu.Do tada neka neko pokuša provesti eksperiment i izvjesti o rezultatu.

Objašnjenje koje je dao @nedeljko nije pogrešno,oj @atelago.

Suština cake je u tome da se u tvom tekstu izjednačuje impuls sile i rad sile.
A to su različiti pojmovi,čak više nego žabe i babe.Inače raketni pogon je objašnjen na bazi zakona o održanju energije,a i svaki drugi koji osmisliš.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{29.12.2012. u 10:22 - pre 150 meseci}

Lupetate i ti i Nedeljko nekim opštim i nekonkretnim frazama koje ne
objašnjavaju ništa.
Dvaput brže telo ima četiri puta veću kinetičku energiju. Zašto?
Ispada da ne znate ni šta je akceleracija.

Možeš ti da uvrštavaš koga hoćeš i gde hoćeš, ali inercijalni i neinercijalni
sistemi nisu Ajnštanovo vlasništvo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{29.12.2012. u 23:03 - pre 150 meseci}

Pri konstantnoj sili rad je srazmeran pređenom putu na kome sila deluje, a ne trajanju njenog delovanja. Raketa je u drugoj ubrzavanja fazi prešla duži put.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu