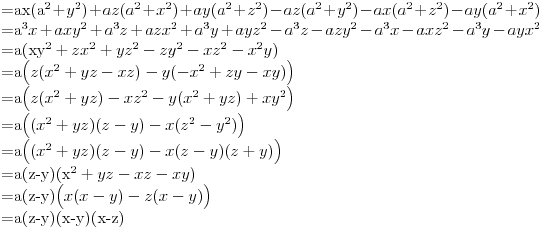Zadatak se može rešiti upotrebom nekih osnovnih svojstava determinante.
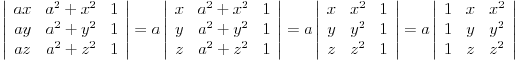
Ovo poslednje je
Vandermondova determinanta
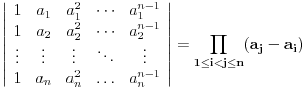
pa je rešenje
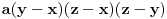
tj.
.
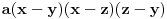
Ako nije jasno šta sam radio:
1. korak: Ako je čitava kolona ili čitava vrsta pomnožena nekim brojem, taj broj se može "izvući" ispred determinante. U konkretnom slučaju izvučen je broj
iz prve kolone.
2. korak: Determinanta ne menja vrednost ukoliko se neka vrsta sabere sa umnoškom neke druge vrste (ili neka kolona sabere sa umnoškom neke druge kolone). U konkretnom slučaju drugoj koloni dodata je treća kolona pomnožena brojem
.
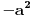
3. korak: Ako dve susedne vrste/kolone zamene mesta - znak determinante se menja. U konkretnom slučaju prvo su mesta zamenile treća i druga kolona, pa nakon toga (novonastala) druga i prva kolona - time je znak determinante promenjen dva puta, pa je isti kao i na početku.
Kako bi rešio zadatak ako ne znaš formulu u vezi sa
Vandermondovom determinantom?
Jedna od mogućnosti je da upotrebiš taktiku koja se i koristi prilikom dokaza pomenute formule:
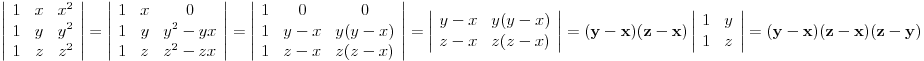
Dakle:
1. korak: Trećoj koloni je dodata druga kolona pomnožena brojem
.
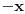
2. korak: Drugoj koloni je dodata prva kolona pomnožena brojem
.
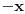
3. korak: Upotrebljen je razvoj po prvoj vrsti (što je naročito zgodno zbog one dve nule).
4. korak: Iz prve vrste izvučen je koeficijent
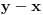
a iz druge vrste koeficijent
[Ovu poruku je menjao uranium dana 25.09.2006. u 11:39 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
Dokazati identitet sa determinantom - koji je drugi način?
da vidimo i jednu varijantu bez njega:
