Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.

Najlepši zadaci

[es] :: Matematika :: Najlepši zadaci
(TOP topic)
Strane: << < .. 4 5 6 7 8 9 10 11 12 13 ... Dalje > >>

[ Pregleda: 291631 | Odgovora: 858 ] > FB > Twit

Postavi temu Odgovori

Autor
Pretraga teme: Traži
Markiranje Štampanje RSS

stalker
Branko Kokanovic
Beograd

Član broj: 11897
Poruke: 606
*.rcub.bg.ac.yu



+2 Profil

icon Re: Najlepši zadaci05.04.2004. u 22:11 - pre 244 meseci
Pa meni nije:) Tj. bar nije bio dok dobro ne razmislis. I sada kada sam umoran mogu da viknem 'Vau'. U stvari, svi mi razmisljamo da je ta verovatnoca namenjena bas tebi, pa svi imaju odgovor 360 i kusur:) Zapravo, tu su kombinacije svako sa svakim, pa i ima logike
 
Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8632
*.dial.InfoSky.Net



+2790 Profil

icon Re: Najlepši zadaci09.04.2004. u 15:09 - pre 244 meseci
Moram priznati da rešenje zadatka sa funkcijom koje je ponudio učesnik koji je pisao o geometrijskom i analitčkom rešenju (sa beskonačnim matricama) nije prihvatljivo, pre svega zato što implicitno zadana funkcija u opštem slušaju nije funkcija, već u nekoj okolini bilo koje tačke koja zadovoljava jednačinu predstavlja funkciju kojom se neka od nepoznatih izražava preko ostalih. Takođe, u rešenju postoji i jedna greška koja nema veze sa postavkom nego sa matričnim računom. Naime, jednakost



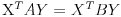
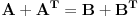
za sve X,Y, gde su A i B kvadratne matrice istog reda, a X i Y kolone odgovarajućeg reda, je ekvivalentna sa , dok se A=B može zaključiti samo u slučaju da su A i B simetrične matrice. Srkijevo rešenje nije dobro jer ima problem sa time gde se slika nula na osnovu svih onih uslova.

Štaviše, može se pokazati da ne postoji neprekidno rešenje, niti rešenje sa konačno mnogo tačaka prekida, tako da i Chupkovo rešenje otpada. Međutim, njihova ideja je dobra, s tim što je trebalo upotrebiti beskonačno mnogo intervala.

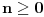
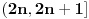
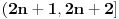
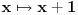
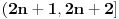
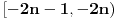
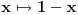
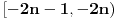
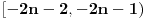
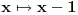
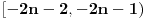
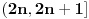
Naime, nulu ćemo preslikati u nulu, a za bilo koji ceo broj preslikaćemo interval na interval sa , interval na interval sa , interval na interval sa i interval na interval sa .

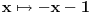
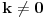
Rešenja naravno ima beskonačno mnogo jer za svako rešenje i realan broj imamo i rešenje .
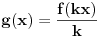
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8632
*.dial.InfoSky.Net



+2790 Profil

icon Re: Najlepši zadaci09.04.2004. u 16:15 - pre 244 meseci
U vezi zadatka da se dokaže da ne postoji diferencijabilna funkcija koja slika prostor u ravan. E pa ne postoji čak ni takva neprekidna funkcija. Naime, u Topologiji postoji takozvana Borsuk Ulamova lema koja je dokazana metodama Algebarske Toplogije a koja zapravo tvrdi mnogo više. Neka je



takozvana (n-1)-dimenziona sfera. Tačke i na njoj zovemo antipodalnim. Za svaku neprekidnu funkciju postoje antipodalne tačke koje se slikaju u istu tačku. Budući da je i da je svaka diferencijabilna funkcija neprekidna, naš zadatak je specijalan slučaj ove teoreme.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
Odgovor na temu

Aleksandar Ilić
Software Developer
Beograd

Član broj: 15867
Poruke: 417

Sajt: www.ailic.rs


+3 Profil

icon Re: Najlepši zadaci13.04.2004. u 17:52 - pre 244 meseci
Koliko sam primetio niko nije dao odgovor na Zadatak 24 pa reko ja da pokusam.

Majka rodila sina sa 21 godinom. Za tacno 6 godina, ali pise u zagradama racunajuci od danas, majka ce biti 5 puta starija od sina. Posto ovo nema nikakve veze jer za 6 godina majka ce imati 27 godina, a sin 6 godina znaci ne uklapa se.
I sad pitanje glasi gde se nalazi tata?
Pa za tacno 6 godina (racunajuci od danas) sin ce puniti 6 godina i znaci tata ce biti na proslavi njegovog sestog rodjendana.

Jesam li u pravu???
„Naposletku, suština saznavanja nije u tome gubimo li igru, već kako je gubimo,
šta time spoznajemo, čemu nas je poraz naučio i kako nas to menja. Gubiti na određen
način znači - dobijati.”
Richard Bach
 
Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8632
*.dial.InfoSky.Net



+2790 Profil

icon Re: Najlepši zadaci13.04.2004. u 19:47 - pre 244 meseci
Ne, nisi u pravu! Ako danas majka ima x godina, za 6 godina će imati ona imati x+6 godina, a njen sin x-21+6=x-15 godina, pa pošto mora biti x+6=5*(x-15), dobijamo da majka sada ima 20,25 godina, tj da će sina roditi za 0,75 goduna=9 meseci, što daje nedvosmislen odgovor gde je (sada) otac. To je na ovom forumu već objasnio Dejan Katašić zvani noviKorisnik.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
Odgovor na temu

Leftist
Luka Stojanovic
Bg

Član broj: 21766
Poruke: 401
*.drenik.net

Jabber: slartibartfast@jabber.cc
Sajt: www.reggae.rs


+5 Profil

icon Re: Najlepši zadaci15.04.2004. u 23:33 - pre 243 meseci
Niko nije resavao 4. zadatak?
Ja se tripujem da sam ga resio, ali nisam dobio jednoznacno resenje. Mogu li da znam da li je to u redu, cisto da ne ispadnem glup u drustvu : )

P.S. Kad sam provalio da ima vise od jednog resenja napravio sam program koji racuna sva moguca, pa i to mogu da postujem, ako je sva ova prica sa vise resenja dobra...
Go Beograd
Reggae Serbia
Black Ark
 
Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.smin.sezampro.yu.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253


+605 Profil

icon Re: Najlepši zadaci15.04.2004. u 23:38 - pre 243 meseci
Kako niko nije rešio 4. zadatak, imaš o njemu toliko materijala da možeš do sutra da čitaš. Samo skokni do http://www.elitesecurity.org/tema/18994 i http://www.elitesecurity.org/tema/28130.
Ljubičice crvena, što si plava kô zelena trava.
 
Odgovor na temu

chupcko
Negde
Beograd

Član broj: 5560
Poruke: 1141

Sajt: www.google.com


+63 Profil

icon Re: Najlepši zadaci21.04.2004. u 08:18 - pre 243 meseci
Malo sam surfao i setio se da je ovde bila rasprava oko onog proizvod suma i ...

Evo nadjoh lepo objasnjeno resenje: pa koga ne mrzi da cita..., takodje ima tu puno lepih zadataka.

http://www.qbyte.org/puzzles/p003s.html
CHUPCKO
 
Odgovor na temu

devojcica

Član broj: 25559
Poruke: 25
*.sr.gov.yu.

Jabber: savic_marijana@yahoo.com


Profil

icon Re: Najlepši zadaci28.04.2004. u 17:18 - pre 243 meseci
Cao, kako vam se svidja ovaj
Code:
Zadatak 26:

Dati su brojevi 1, 3, 4, 6. Treba da se dobije 24 koristeci samo operacije +, -, *, /  i
svaki od datih brojeva tacno jedanput.
 
Odgovor na temu

srki
Srdjan Mitrovic
Auckland, N.Z.

Član broj: 2237
Poruke: 3654
..-chandran.sbs.auckland.ac.nz



+3 Profil

icon Re: Najlepši zadaci29.04.2004. u 00:26 - pre 243 meseci
Znaci ne smeju da se koriste zagrade? I ne sme na pocetku da bude "-" posto se "-" koristi samo kao operacija?
 
Odgovor na temu

noviKorisnik
Dejan Katašić
Novi Sad

Član broj: 13216
Poruke: 4533
*.dialup.neobee.net.

Sajt: www.novikorisnik.net


+5 Profil

icon Re: Najlepši zadaci29.04.2004. u 01:32 - pre 243 meseci
Teško... Ima 4 operanda i 4 operacije!
Za 4 operanda dovoljne su 3 operacije. 4 operacije zadovoljava 5 operanda.
Ali, u tekstu nije napomenuto da moraju da se koriste sve 4 operacije (samo se kaže da se koriste svi operandi) - tako da mogu da se koriste i samo 3 operacije.
BoxUp
interesantna logička igra
Monty Hall paradoks - interaktivni demo
 
Odgovor na temu

devojcica

Član broj: 25559
Poruke: 25
*.sr.gov.yu

Jabber: savic_marijana@yahoo.com


Profil

icon Re: Najlepši zadaci29.04.2004. u 16:10 - pre 243 meseci
Smeju da se koriste zagrade, i operacije gde god i koliko god puta je potrebno (ukljucujuci 0 puta i - kao unarnu operaciju, tj. na pocetku).
 
Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2154
*.dialup.blic.net



+196 Profil

icon Re: Najlepši zadaci29.04.2004. u 23:50 - pre 243 meseci
Ovo je jako teško riješiti.Ja sam nešto napravio,ali..
da li je dobro?Saćekaću.
________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]
 
Odgovor na temu

blaza
n/a

Član broj: 961
Poruke: 743
*.vdial.verat.net



+3 Profil

icon Re: Najlepši zadaci29.04.2004. u 23:55 - pre 243 meseci
6*4-3-1=24
naravno, u oktalnom brojnom sistemu.
O_o
 
Odgovor na temu

stalker
Branko Kokanovic
Beograd

Član broj: 11897
Poruke: 606
*.drenik.net



+2 Profil

icon Re: Najlepši zadaci30.04.2004. u 00:35 - pre 243 meseci
(14-6)*3
naravno u decimalnom...
 
Odgovor na temu

blaza
n/a

Član broj: 961
Poruke: 743
*.vdial.verat.net



+3 Profil

icon Re: Najlepši zadaci30.04.2004. u 01:41 - pre 243 meseci
Dati su brojevi 1, 3, 4, 6, a ne cifre 1, 3, 4, 6.
O_o
 
Odgovor na temu

srki
Srdjan Mitrovic
Auckland, N.Z.

Član broj: 2237
Poruke: 3654
..-chandran.sbs.auckland.ac.nz



+3 Profil

icon Re: Najlepši zadaci30.04.2004. u 02:53 - pre 243 meseci
posto 6 moze da se okrene naopako da ispadne 9 onda bi resenje moglo da bude:
(1+4)*3+9
 
Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.mobtel.co.yu

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253


+605 Profil

icon Re: Najlepši zadaci30.04.2004. u 03:16 - pre 243 meseci
Ili .
Ljubičice crvena, što si plava kô zelena trava.
 
Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8632
*.dial.InfoSky.Net



+2790 Profil

icon Re: Najlepši zadaci30.04.2004. u 13:32 - pre 243 meseci
Nadam se da na ovo rešenje niko neće imati primedbi.

6 / (1 - (3 / 4)) = 24.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
Odgovor na temu

devojcica

Član broj: 25559
Poruke: 25
*.sr.gov.yu.

Jabber: savic_marijana@yahoo.com


Profil

icon Re: Najlepši zadaci30.04.2004. u 14:09 - pre 243 meseci
Da to je bilo planirano resenje, ali mi se mnogo svidja ovo oktalno. Za Bojana, nije bilo dozvoljeno stepenovanje.
 
Odgovor na temu

[es] :: Matematika :: Najlepši zadaci
(TOP topic)
Strane: << < .. 4 5 6 7 8 9 10 11 12 13 ... Dalje > >>

[ Pregleda: 291631 | Odgovora: 858 ] > FB > Twit

Postavi temu Odgovori

Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.