Dragi uraniume, nema nikakve nesuglasice
Elem:
Citat:
uranium: s obzirom na negativno rešenje problema trisekcije ugla, u kom obliku tražimo rešenje?
Nadam se da ćeš se složiti da je sledeći izraz tačan:
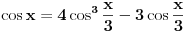
(dobija se sasvim lako iz prvog izraza koji si napisao u svojoj prvoj poruci).
Sada ja pitam: Pošto je po
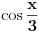
ovo kubna, te stoga i rešiva jednačina, zanima me da li je neko negde nekad "ispešačio" to rešenje i napisao ga u obliku koji obuhvata konačan broj zbirova, razlika, proizvoda, količnika, kvadratnih korenova i kubnih korenova realnih brojeva i trigonometrijskih funkcija od
.
Pitanje zaista nema reperkusija na (ne)izvodljivost trisekcije ugla pomoću lenjira i šestara, jer ne tražimo geometrijsku konstrukciju kubnog korena (za koju, dao bog, znamo da je nemoguća
).
[Ovu poruku je menjao Farenhajt dana 24.12.2005. u 23:01 GMT+1]
Trigonometrija - adicione formule
