Početna dužina trake je

. Mrav se kreće konstantnom brzinom

. Za vreme

, mrav pređe put
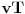
. Neka su trenuci
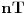
, upravo oni trenuci kada se traka trenutno izdužuje za jednu svoju početnu dužinu

, gde je

prirodan broj. Mrav nema dimenzije, tj. mrav je, u stvari, materijalna tačka.
Iz perspektive mrava, ne dešava se ništa posebno - u svakom periodu (od
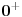
do
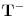
, od
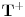
do
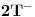
, itd...) on prelazi isti put dužine
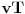
. Samo što to konstantno postignuće malog mrava, u svakom sledećem periodu vredi sve manje i manje.
Posmatrajmo sam trenutak

. Budući da mrav nema masu, nema dimenzije i da se traka isteže trenutno, u relativnom smislu nema nikakve promene: neposredno pre istezanja (trenutak
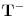
), traka je bila dužine

, a mrav je prešao put
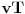
. Neposredno posle istezanja (trenutak
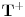
), traka je bila dužine
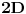
, a mrav je prešao put
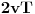
, jer ga je ponela sama traka. Okreni, obrni, mrav je prešao jednom za svagda
jedan određeni procenat ukupnog puta. Na kraju sledećeg perioda (trenutak
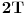
), na tu osnovnu
jedinicu, u procentima, dodaje se
polovina te osnovne jedinice, opet u procentima - on mučenik zaradio
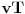
, ali su sve cene dvostruko veće od onih u istom periodu prošle godine - sada su
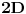
,... što nas dovodi do zaključka da mrav, u relativnim jedinicama, prelazi put po zakonu
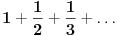
.
Pošto je osnovna relativna jedinica pređenog puta
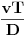
, naše pitanje, u stvari, glasi:
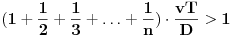
, tj. za koje n važi:
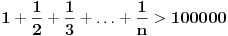
, jer je
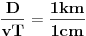
Gruba procena kaže da je n broj između 2^100000 i 2^200000 => svemir je previše mlad da bi se ovo desilo....