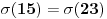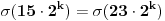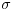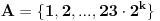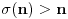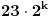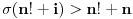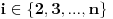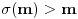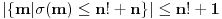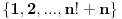• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike
• Jabber
• Email
• Chat

• elitesecurity ::
• elitemadzone ::
• WAP ::
• EMAIL ::
• NEWS ::
• RSS

  Niste ulogovani?  Username :   Password:   

• Registracija
• Izgubili ste password?
• Flashback ▲▼

Pretraga:  

Srodne teme 12.09.2002. matematika 21.01.2004. Zadatak sa opstinskog takmicenja 19.02.2004. problem sa matricama 17.08.2004. Pomoc oko sum() i mysql 16.01.2005. Zeza me jedan zadatak 03.02.2005. algoritam - pomoc! 28.02.2005. Jedan zadatak sa olimpijade 09.03.2005. Po kozna koji put Ulaz-Izlaz na izveštaju. MOLIM! Navigacija Brisanje liste Aktuelne teme u ovom forumu: pomoc oko inegrala Zadatak sa Paskalovom tj Briansonovom .. Preporuka "naprednijeg" kalk.. Pomoć oko Verovatnoće IMO tim Srbije rezultati Jednacina, ko je rijesi svaka cast ali.. Faktoriel racionalnog broja? pomoc oko zadataka iz redova pomoc oko jos jednog integrala! Problem sa integralom (ovoga puta uspe.. Racionalni algebarski izrazi -POMOC !:) matematicka logika Molim pomoć hitno oko jednog zadatka. Prirodno Matematicki Fakultet [savjet] matematicki program Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Windows aplikacije :: Browseri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Enterprise Networking Home Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Virtualizacija .NET 3D programiranje Art of Programming Asembler C programiranje C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python & Zope Visual Basic 6 Veštačka inteligencija XML GameDev - Razvoj Igara Ostali programski jezici C programiranje :: C za početnike PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: .NET Presentation Foundation C++ programiranje :: C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Kriptografija i enkripcija Security Security Coding Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - tržište GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile GSM - tržište :: Nokia GSM - tržište :: Samsung GSM - tržište :: Siemens GSM - tržište :: SonyEricsson GSM - tržište :: Motorola GSM - tržište :: LG PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP E-mail File Sharing Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Instant Messaging :: Jabber i XMPP Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike E-Marketing :: Affiliate Programi Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni foto-aparati Digitalne kamere Digitalni foto-aparati :: Fotografija Elektronika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Berza IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice BalkanSat Digitalna Televizija BalkanSat :: Dreambox, Samsung, Humax, D.. BalkanSat :: PC DVB kartice Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone AutoZone MotoZone MadZone :: Zanimljivi linkovi MadZone :: Svakodnevnica TechZone :: Ergonomija TechZone :: Klimatizacija i bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

Bojan Basic Novi Sad SuperModerator Član broj: 6578 Poruke: 3636 *.dialup.neobee.net. Jabber: bojan_basic@elitesecurity.org ICQ: 305820253 Profil [Zadatak]: Suma delilaca 15.03.2005. u 12:49 Dokazati da postoji beskonačno mnogo brojeva takvih da 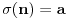nema rešenja, gde je 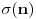suma delilaca broja . Ja znam dva rešenja ovog problema, jedno dosta komplikovano i prilično "brute force" dok je drugo izuzetno elegantno. Može li neko rešiti ovo na možda treći način? :) Ljubičice crvena, što si plava kô zelena trava. 15.03.2005. u 12:49

gpreda Goran Predovic Kragujevac Član broj: 19087 Poruke: 74 212.200.23.* Sajt: alas.matf.bg.ac.yu/~mr990.. Profil Re: [Zadatak]: Suma delilaca 15.03.2005. u 14:08 Ovo mi je prvo palo na pamet: Posmatrajmo preslikavanje skupa , bar vrednosti ce se ponavljati (gornje jednakosti). Kako je , zakljucujemo da postoji najmanje celih brojeva manjih od za koje jednacina nema resenja. 15.03.2005. u 14:08

Bojan Basic Novi Sad SuperModerator Član broj: 6578 Poruke: 3636 *.dialup.neobee.net. Jabber: bojan_basic@elitesecurity.org ICQ: 305820253 Profil Re: [Zadatak]: Suma delilaca 15.03.2005. u 15:46 Lepo. Evo još jedne slične konstrukcije. Primećujemo da je za sve . Pošto je sledi da je . Dakle, postoji bar brojeva u skupu takvih da nema rešenja. Ljubičice crvena, što si plava kô zelena trava. 15.03.2005. u 15:46