Pretpostavljam da hoćeš da kažeš „skup pozitivnih realnih brojeva“ umesto „pozitivan realan broj“.
Odgovor na postavljeno pitanje je da. Dokazaću ovo na dva načina, od kojih prvi pokazuje eksplicitnu konstrukciju traženih podskupa a drugi je tu samo zanimljivosti radi, jer se rešenje dobija u jednom koraku pozivanjem na specijalan slučaj jedne vrlo lepe (ali i vrlo teške) teoreme.
1) Prvi način:
Najpre ćemo podeliti skup
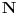
na traženi način. Neka su definisani sledeći skupovi:
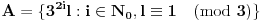
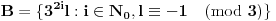
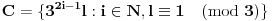
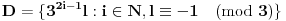
Dokazaćemo da ovi skupovi zadovoljavaju uslove zadatka. Pretpostavimo da postoje
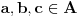
za koje važi
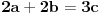
. Imamo sledeće:
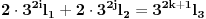
Neka je
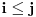
.
Ukoliko je
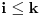
deleći sve sa
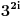
imamo:
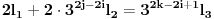
Pošto je desna strana deljiva sa

, mora biti
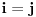
. Tada važi:
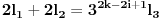
S druge strane, kako je
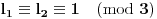
sledi da leva strana nikad ne može biti deljiva sa

. Kontradikcija.
Još lakše, ukoliko je

, deleći sve sa
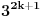
imamo:
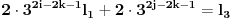
pa je leva strana deljiva sa

a desna nije.
Analogno se pokazuje da data jednačina nije rešiva ni u ostalim podskupima.
Za
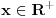
koristićemo oznake
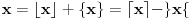
, gde su sa
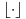
i

standardno označeni donji i gornji ceo deo, redom. Za
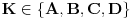
i
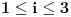
označimo:
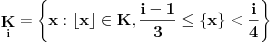
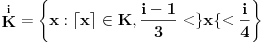
Potrebna su nam još dva skupa, naime:
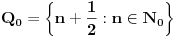
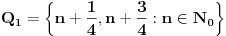
Lako se proverava da su svi ovi skupovi međusobno disjunktni i da je
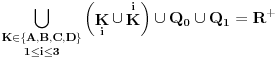
. Preostaje još da se dokaže da jednačina
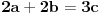
nije rešiva ni u jednom od njih.
Neka
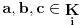
i pretpostavimo da važi
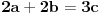
. Tada:
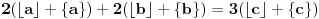
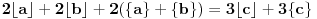
Iz ograničenja sledi
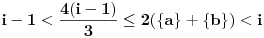
i
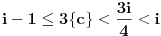
, odakle zaključujemo da mora važiti
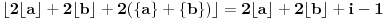
i
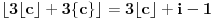
pa je
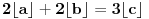
što je nemoguće na osnovu već dokazanog jer

.
Slično, ako
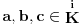
i
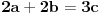
onda imamo:
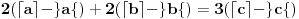
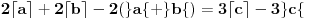
Pošto je
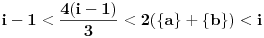
i
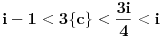
sledi
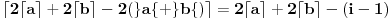
i
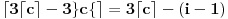
, odnosno
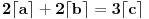
što je nemoguće, slično malopređašnjem objašnjenju.
I poslednje, ako
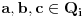
onda je leva strana jednakosti ceo broj a desna nije, pa jednačina nema rešenja ni u ovom skupu.
Za kraj samo da napomenem da, kao što se može prebrojati, ovo rešenje uključuje
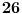
podskupa. Ovo nikako nije minimum, štaviše relativno jednostavnom modifikacijom ovo rešenje možemo svesti na
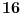
podskupa, ali sam se odlučio za ovo jer je prirodnije a broj podskupa ne igra veliku ulogu.
2) Drugi način:
Definicija 1:
Neka
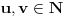
i neka je

matrica
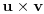
sa elementima iz
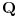
. Neka je

potpolugrupa od
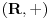
. Tada kažemo da za

važi
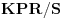
(
kernel partition regular over 
) akko kad god je
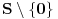
obojen sa konačno mnogo boja postoji monohromatski
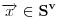
takav da je
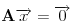
.
Definicija 2:
Neka
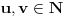
i neka je

matrica
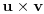
sa elementima iz
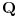
. Označimo kolone od

sa
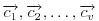
. Tada

zadovoljana
uslov kolona akko postoji
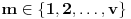
i particija
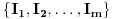
skupa
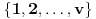
u neprazne podskupe takva da važi:
a)
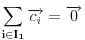
;
b) za svako
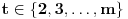
,
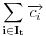
je linearna kombinacija sa koeficijentima iz
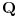
vektora iz
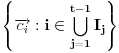
.
Teorema: (Rado)
Neka
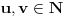
i neka je

matrica
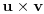
sa elementima iz
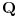
. Sledeći iskazi su ekvivalentni:
a)

je
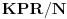
;
b)

je
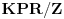
;
c)

je
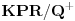
;
d)

je
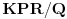
;
e)

je
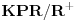
;
f)

je
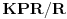
;
g)

zadovoljava uslov kolona.
Primenom ove teoreme rešenje zadatka dobijamo u jednom koraku. Zaista, neka je
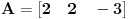
Nemoguće je zadovoljiti uslov a) iz Definicije 2, pa sledi da

ne zadovoljava uslov kolona, pa iz Teoreme dobijamo da nije
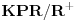
, što je ekvivalentno pitanju iz zadatka.
Da vidimo još neke zanimljive posledice Radove teoreme.
Šurova teorema:
Za svako bojenje skupa
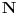
u konačno mnogo boja postoje
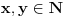
takvi da su
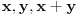
iste boje.
Dokaz:
Primenimo Radovu teoremu na matricu
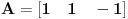
koja zadovoljava uslov kolona.
Van der Waerden's Theorem:
Za svako bojenje skupa
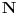
u konačno mnogo boja postoji konačna monohromatska aritmetička progresija proizvoljno velike dužine.
Dokaz:
Pretpostavimo da želimo da pokažemo da postoji aritmetička progresija dužine

(slično ide za bilo koju dužinu). Neka je
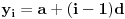
za
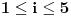
. Tada od sistema jednačina:
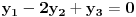
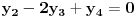
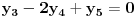
pravimo sledeću matricu:
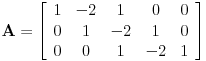
Zbir svih kolona ove matrice je
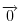
pa ona zadovoljava uslov kolona. Ipak, život nam nije tako lep pošto sve što nam Radova teorema garantuje u ovom slučaju je da postoji aritmetička progresija makar sa
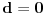
, što nije ono što nas zanima. Ovo se da lako popraviti, naime možemo staviti
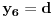
i tražiti da i ono bude iste boje iz jednačine
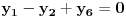
Tada je
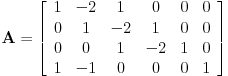
koja zadovoljava uslov kolona kad uzmemo
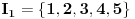
i
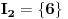
.
Literatura:
[1] R. Rado,
Studien zur Kombinatorik, Math. Zeit.
36 (1933), 242-280.
[2] R. Rado,
Note on combinatorial analysis, Proc. London Math. Soc.
48 (1943), 122-160.
[Ovu poruku je menjao Bojan Basic dana 19.04.2006. u 02:09 GMT+1]
Ljubičice crvena, što si plava kô zelena trava.