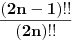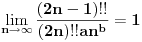Mene je interesovala veza (ako ona postoji) izmedju formula
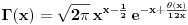
i
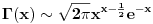
. Da li se iz jedne od ovih formula moze doci do druge? I uopste, da li postoji neka prica (ne vezano za Stirlinga) kako mozemo sa asimptotske relacije da predjemo na nesto sto je aproksimirano sa nizom ili pak funkcijom (kako je ovde ucinjeno)?
Nije mi poznat pojam "Asimptotskog razvoja" (moram priznati), pogledao sam malo na internetu i u sustini sam video sta je filozofija.
Ja sam formulu
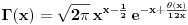
nasao kod Kadelburga (ali, bez dokaza), gde je receno da se dokaz moze naci kod
Code:
Matematičeskiй analiz (V.A. Ilьin, V.A. Sadovničiй, Bl.H. Sendov),
gde se mogao naci dokaz za formulu
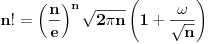
, gde

.
Zatim je data napomena, da se moze pokazati
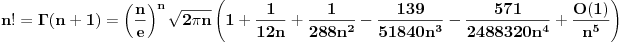
(sto doduse pise i na wikipediji), i da se to moze naci kod
Code:
Osnovы matematičeskogo analiza. V 2-h č. Ilьin V.A., Poznяk Э.G.
Tako da sam video ono sto me je zanimalo.
I hvala na trudu obojici.
nema potrebe da se odgovara na gornja pitanja (sem ako bas ne zelite), ne znam ni sto sam ih postavio (al neka stoje tu, necu ih brisati)
Leonardo da Vinči
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.