Dakle, skup konstruktibilnih brojeva
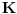
je zatvoren za operacije sabiranja, oduzimanja, množenja, deljenja, kvadratnog korenovanja. (Znači možeš ih izvršiti konačno mnogo puta na elementima skupa
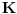
i kao rezultat dobiti opet element skupa
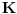
)
E sad, ako bi našao opštu formulu koja je dobijena primenom konačno mnogo nabrojanih operacija, ona bi trebalo da važi za sve uglove, pa između ostalih i za one čiji je kosinus konstruktibilan a kosinus trećine nekonstruktibilan i tako bi došlo do kontradikcije.
U ovom trenutku mogu samo da nagađam, da li se dotični trik može uopštiti tj. da li se može konstruisati neko nadpolje
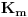
od
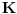
tako da obuhvati i sve brojeve oblika
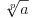
,
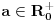
, za svako prosto

za koji važi
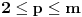
, a nakon toga "izvući iz šešira" neko zgodno
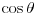
koje ne pripada datom skupu
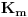
.
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.