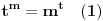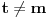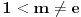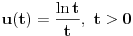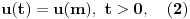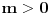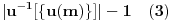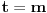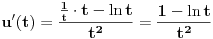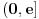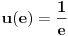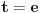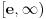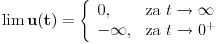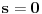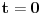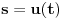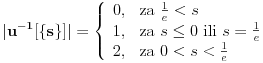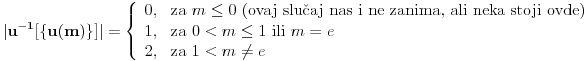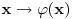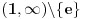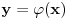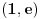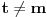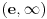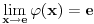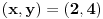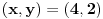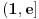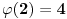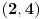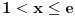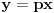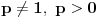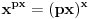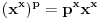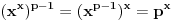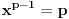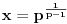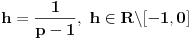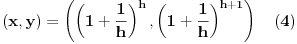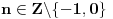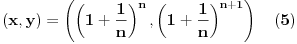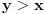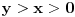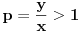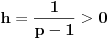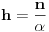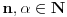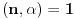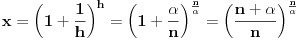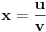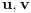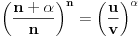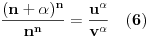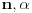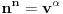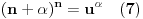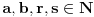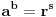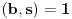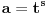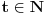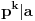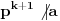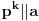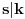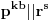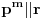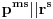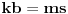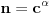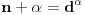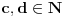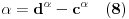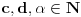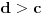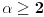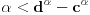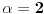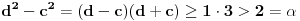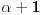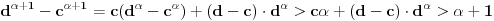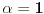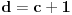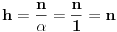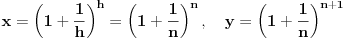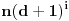Ja ću da dam malo obimniju diskusiju zadatka 2, nadam se da neću (previše) smoriti.
Za početak, tražimo realna rešenja jednačine
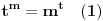
, gde je

nepoznata a

parametar (obe veličine su pozitivne).
Tvrđenje 1:
Postoji rešenje
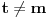
jednačine (1) ako i samo ako je
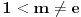
, i za takvo

to rešenje je jedinstveno.
Dokaz:
Neka je
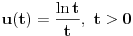
. Logaritmujući vidimo da je jednačina (1) ekvivalentna sa
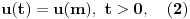
(gde je
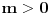
parametar). Broj rešenja jednačine (2) jednak je
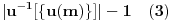
(jedinicu oduzimamo da ne bismo računali trivijalno rešenje
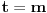
). Dalje, pošto je
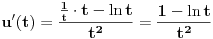
sledi da

raste na intervalu
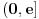
, dostiže maksimum
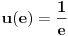
u
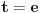
, i opada u intervalu
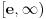
. Pošto je
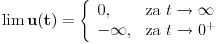
sledi da su prave
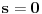
i
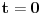
horizontalna i vertikalna asimptota funkcije
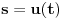
, redom. Dakle,
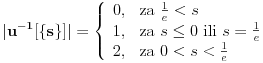
pa je i
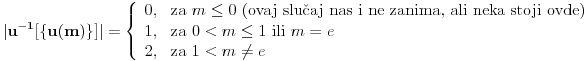
Zaključak sada sledi iz (3).
Na osnovu tvrđenja 1 sledi da možemo definisati funkciju
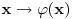
koja preslikava domen
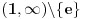
na samog sebe, takvu da
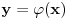
predstavlja jedinstveno netrivijalno rešenje jednačine
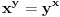
. Takođe primetimo da možemo da zamenimo mesta promenljivama

i

. Sada, posmatrajući grafik funkcije
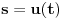
(definisan u dokazu tvrđenja 1), primećujemo da dok

raste u
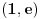
odgovarajuće
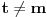
opada u
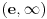
, i obratno. Dakle,

strogo opada na celom svom domenu. Osim toga, možemo proveriti da je
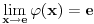
, pa ćemo ovo baš ovako i definisati. Ovo nam omogućuje da rešimo prvi deo zadatka:
a) Jedina netrivijalna prirodna rešenja posmatrane jednačine su
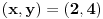
i
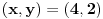
.
Dokaz:
Pošto je

jedini prirodan broj u intervalu
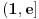
i
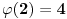
,
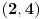
je jedina celobrojna tačka grafika
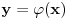
za
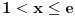
. Simetrijom dobijamo i drugo navedeno rešenje.
Napomena:
Ovaj deo zadatka mogao se rešiti i sasvim elementarno, međutim takvo rešenje se ne bi moglo dalje uopštiti, pa sam odlučio da napišem ovu varijantu. Ukoliko nekoga ipak zanima i elementarno rešenje neka se javi na ovoj temi pa ću i to ispisati.
Dalje, neka je za netrivijalno rešenje posmatrane jednačine
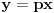
za neko

. Važi
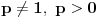
i
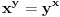
može biti napisano u obliku
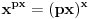
odnosno
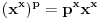
pa je
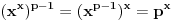
iz čega sledi
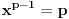
pa nalazimo da je
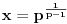
. Neka je
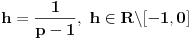
. Tada možemo zapisati rešenja jednačine u parametarskom obliku:
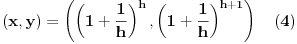
Primetimo da su za
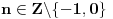
rešenja data sa
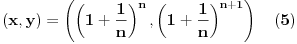
zapravo netrivijalna racionalna rešenja posmatrane jednačine. Prelazimo na rešavanje drugog dela zadatka.
b) Sva racionalna rešenja posmatrane jednačine data su parametrizacijom (5).
Dokaz:
Bez umanjenja opštosti možemo pretpostaviti da je
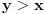
. Dakle, neka je
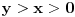
racionalno rešenje date jednačine. Onda je i
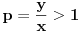
racionalan, kao i
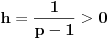
. Neka je
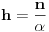
tako da
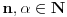
i
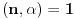
. Na osnovu (4) imamo:
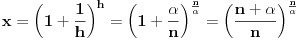
Neka je
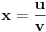
gde su
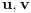
prirodni, uzajamno prosti brojevi. Sada imamo
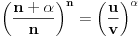
iz čega sledi:
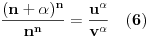
Kako su
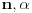
i
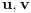
uzajamno prosti, sledi da su oba razlomka u (6) neskrativi. Dakle:
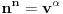
i
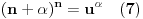
Dalje nam treba sledeća lema.
Lema 1:
Neka su
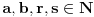
takvi da je
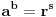
. Ako je
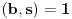
onda je
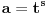
za neko
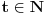
.
Dokaz:
Dovoljno je dokazati da ako je

prost činilac broja

takav da
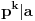
i
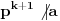
(ovo ćemo dalje beležiti sa
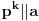
), onda
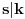
. Pošto je
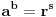
, vidimo da važi
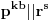
. Ako je
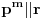
, onda
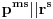
, pa je
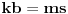
. Iz pretpostavke
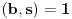
sledi
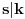
.
Primenom leme 1 dva puta na (7) dobijamo da je
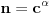
i
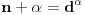
za neke
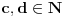
. Dakle,
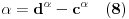
Dokazujemo još jednu lemu.
Lema 2:
Za
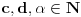
sa
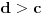
i
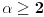
važi
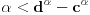
.
Dokaz:
Radimo indukcijom po

. Za
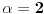
imamo
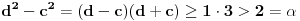
. Sada pretpostavimo da tvrđenje važi za

i dokazujemo da važi za
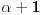
.
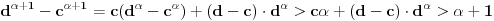
Iz ove leme sledi da jednakost (8) može biti zadovoljena samo za
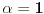
(i tada je
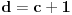
). Dakle,
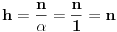
i
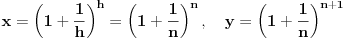
Ovim je zadatak rešen.
Ko je sve pročitao svaka mu čast :)
edit: ispravljene omaške u kucanju na koje je kolega uranium skrenuo pažnju
[Ovu poruku je menjao Bojan Basic dana 07.02.2009. u 02:23 GMT+1]
Ljubičice crvena, što si plava kô zelena trava.
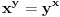 takva da je
takva da je 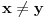
 ;
; .
.



 Elementarna teorija brojeva
Elementarna teorija brojeva