Postoji i opštiji pristup za rešavanje ovih problema.
Prvo, analitička funkcija čiji skup nula ima bar jednu tačku nagomilavanja u unutrašnjosti oblasti je konstantna u celoj oblasti. Iz toga i Tejlorove teoreme sledi da za ma koju nekonstantnu analitičku funkciju
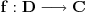
, gde je
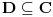
neka oblast i svaku unutrašnju tačku
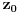
oblasti

postoje

i analitička funkcija
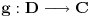
takvi da je
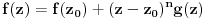
i
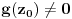
. Odatle sledi da slika bilo koje okoline tačke
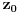
obuhvata sve tačke neke okoline tačke
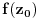
, odnosno da je slika otvorenog i povezanog skupa pri nekonstantnom analitičkom preslikavanju otvoren i povezan skup (povezanost sledi otuda što je slika povezanog skupa pri neprekidnom preslikavanju povezan skup).
Zaista, najpre postoji analitička funkcija
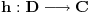
takva da je
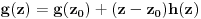
. Neka je dato

takvo da
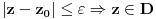
. Za neko
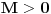
važi
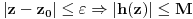
. Neka je
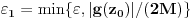
. Tada važi
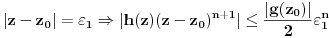
. Neka je
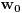
proizvoljan kompleksan broj takav da je
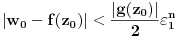
. Dokažimo da postoji
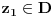
takvo da je
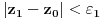
i
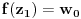
.
Zaista,
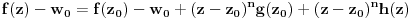
, kao i
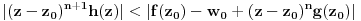
za
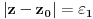
, pa je prema Rušeovoj teoremi dovoljno dokazati da je
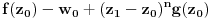
za neko
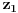
za koje je
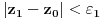
. Ta jednačina je ekvivalentna sa
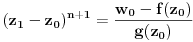
. No, traženo rešenje postoji zbog
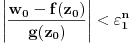
.
[Ovu poruku je menjao Nedeljko dana 11.11.2010. u 19:18 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.