[es] - Najlepši zadaci

Zoran Milovanovic

Član broj: 45186
Poruke: 1206
*.exe-net.net.

+159 Profil

^{29.01.2009. u 22:27 - pre 185 meseci}

ptak. 13 daj tvoju skicu da vidim da li sam dobro razumeo, jer ja sam nasao 4 kvadrata koji su u krug poredjani, a samim tim u sredini se dobija izgled jos jednog, ali njega ne mogu da ubrijim jer on ima 4 zajednicka temena... :)

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+605 Profil

Re: Najlepši zadaci

^{29.01.2009. u 22:31 - pre 185 meseci}

Ali onda nikoja dva nemaju dva zajednička temena, samo po jedno.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Zoran Milovanovic

Član broj: 45186
Poruke: 1206
*.exe-net.net.

+159 Profil

Re: Najlepši zadaci

^{29.01.2009. u 22:43 - pre 185 meseci}

lol, koja ispala... pa kazem ja da je meni nesto cudno tu :)

bruka :)

Odgovor na temu

Tea94
Novi Sad

Član broj: 204478
Poruke: 18
82.117.202.*

Profil

Re: Najlepši zadaci

^{29.01.2009. u 22:43 - pre 185 meseci}

ovako sam ja to zamislila... stavis 1 kvadrat u sredinu, i 4 oko njega... i onda svi oni imaju po 2 zajednicka temena sa ovim u sredini...

Odgovor na temu

ptak 13.
Adamovic Nikola
Srbija - Nis

Član broj: 143532
Poruke: 1476
79.101.220.*

Sajt: putujsaosmehom.blogspot.c..

+284 Profil

Re: Najlepši zadaci

^{29.01.2009. u 22:43 - pre 185 meseci}

Evo ja sam uradio ovako, ne znam da li je tacno, ali nigde se ne spominje da moraju biti jednaki ?!

Aj da cujem misljenja.....
I u AutoCAd sam morao da crtam

Da bi bio genije moras biti bar malo lud. Covek koji je genije, a to ne zna, verovatno i
nije.

Odgovor na temu

Tea94
Novi Sad

Član broj: 204478
Poruke: 18
82.117.202.*

Profil

Re: Najlepši zadaci

^{29.01.2009. u 23:03 - pre 185 meseci}

sta reci... bravo...
ae sad nesto novo...
Ovu je zagonetku Albert Einstein sastavio u 20. stoljeću. Tvrdio je da je moze rijesiti samo 2% svjetske populacije.
Zadatak s kojim se morate suočiti:
1. Postoji pet kuća i svaka je različite boje.
2. U svakoj kući živi po jedna osoba različite nacionalnosti.
3. Stanar svake kuće ima svoje omiljeno piće.
4. Stanar svake kuće ima omiljenu marku cigareta.
5. Stanar svake kuće ima neku kućnu životinju.
Pitanje: Čiji je zec ?

Detalji:
Britanac živi u crvenoj kući.
Šveđanin ima psa.
Danac voli piti čaj.
Zelena kuća lijevo je od bijele.
Vlasnik zelene kuće pije kavu.
Pušač Pall Mall-a drži pticu.
Čovjek koji živi u srednjoj kući pije mlijeko.
Vlasnik žute kuće puši Dunhill.
Norvežanin stanuje u prvoj kući.
Pušač Marlbora stanuje pokraj onoga koji ima mačku.
Čovjek koji ima konja stanuje pokraj onoga koji puši Dunhill.
Čovjek koji puši Winston rado pije pivo.
Norvežanin stanuje pokraj plave kuće.
Nijemac puši Rothmanns.
Čovjek koji puši Marlboro ima susjeda koji pije vodu.

Odgovor na temu

ptak 13.
Adamovic Nikola
Srbija - Nis

Član broj: 143532
Poruke: 1476
79.101.220.*

Sajt: putujsaosmehom.blogspot.c..

+284 Profil

Re: Najlepši zadaci

^{29.01.2009. u 23:11 - pre 185 meseci}

Da ovo je Anstajnov test intalegencije.....radio sam ga pre oko godinu dana i resio za sat-dva vremena....tacno je da je receno da samo 2% ljudi moze da ga resi, ali ja u to sumnjam, evo okacicu sad resenje, samo da ga iskopam. Radio sam to davno postoji program napisan u Delphy-u za to i evo ako nadjem resenje po silnim resenjima u paprnom obliku skeniram i kacim....dok ne nadjem mucite se malo....nije bas lako ! ! !
Ajde necu jso da kacim resenje....da vidim hoce li iko da resi

heheh, nasao sam resenj....poslacu ti na PP, a ovde necu jos da kacim
Srecno svima ! ! !

Da bi bio genije moras biti bar malo lud. Covek koji je genije, a to ne zna, verovatno i
nije.

Odgovor na temu

Tea94
Novi Sad

Član broj: 204478
Poruke: 18
82.117.202.*

Profil

Re: Najlepši zadaci

^{29.01.2009. u 23:14 - pre 185 meseci}

pise 2%, ali ako sam JA uspela da resim, moze bilo ko

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2154
92.241.128.*

+196 Profil

Re: Najlepši zadaci

^{29.01.2009. u 23:48 - pre 185 meseci}

Da nije možda: svaki sa svakim ima po dva zaj.tejmena, a neko tjeme može biti zajedničko
za više kvadrata.Kvadrati ne moraju biti jednaki.Ili da uvedemo pravilo umjetničke slobode.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Prikačeni fajlovi

Zajtem.GIF - 4.97k

Odgovor na temu

ptak 13.
Adamovic Nikola
Srbija - Nis

Član broj: 143532
Poruke: 1476
79.101.220.*

Sajt: putujsaosmehom.blogspot.c..

+284 Profil

Re: Najlepši zadaci

^{29.01.2009. u 23:55 - pre 185 meseci}

Citat:

zzzz: Da nije možda: svaki sa svakim ima po dva zaj.tejmena, a neko tjeme može biti zajedničko
za više kvadrata.Kvadrati ne moraju biti jednaki.Ili da uvedemo pravilo umjetničke slobode.

Jao, jao, jao.....
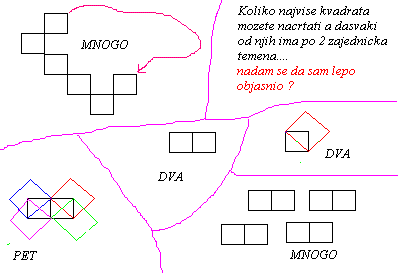
Pazi svaki kvadrat mora da sa drugim ima 2 zajednicka temena.....pa da ti objasnim....
kazes "mnogo" ok koje zajednicko teme imaju prvi dole i treci ? nijedno
"dva" OK, ali moze i 3 kao kod mene.
"pet" Koje zajednicko teme imaju zeleni i plavi kvadrat ? znaci ne moze......to resenje ne moze....
"dva" Ok moze i 3
"Mnogo" pa sta vise puta po dva, to nije resenje.....

Znaci ima dva dobra resenja ali moze i vise.....sto sam dokazao gore.
A ovo ostalo nema veze sa zadatkom.....
Znaci prvi kvadrat mora imati dva temena zaednicka sa drugim, onda drugi sa trecim, treci sa prvim....kontas ?????

Da bi bio genije moras biti bar malo lud. Covek koji je genije, a to ne zna, verovatno i
nije.

Odgovor na temu

mjux

Član broj: 124150
Poruke: 158
79.101.87.*

+2 Profil

Re: Najlepši zadaci

^{30.01.2009. u 00:27 - pre 185 meseci}

nemac ima zeca

Odgovor na temu

Daniel011
Beograd

Član broj: 76088
Poruke: 1101
*.dynamic.sbb.rs.

ICQ: 2336441

+3 Profil

Re: Najlepši zadaci

^{30.01.2009. u 17:57 - pre 185 meseci}

O Ajnštajnovom zadatku je već bilo reči u ovoj temi.

Citat:

Zoran Milovanovic: @zzzz

Mislim da ti ipak nisi dobro razumeo.

Ja mislim da jeste dobro razumeo, jer je zadatak prvobitno bio tako neprecizno formulisan da je mogao da se tumači i na taj način, tj. da svaki kvadrat ima tačno dva temena koja su zajednička sa nekima od ostalih kvadrata. Tek naknadno je objašnjeno da se traži da svaki kvadrat treba da sa svakim kvadratom ima dva zajednička temena.

Odgovor na temu

Zoran Milovanovic

Član broj: 45186
Poruke: 1206
*.exe-net.net.

+159 Profil

Re: Najlepši zadaci

^{30.01.2009. u 19:26 - pre 185 meseci}

Ok, never mind...

http://www.elitesecurity.org/t28555-20#2183483 <----click

pored boldovanog teksta dve reci u levo pise "dasvaki od", ja stvarno ne znam kako ces ti to da tumacis. Ali sem sto fali razmak, sve ostalo je jasno!

Odgovor na temu

ptak 13.
Adamovic Nikola
Srbija - Nis

Član broj: 143532
Poruke: 1476
212.200.194.*

Sajt: putujsaosmehom.blogspot.c..

+284 Profil

Re: Najlepši zadaci

^{30.01.2009. u 20:10 - pre 185 meseci}

Ljudi da li sam ja nepismen ili sta je u pitanju ?
Nisam editovao post, zadatak je dovoljno jasan i ja sam da omoguce resenje, mozda postoji jos koje....ne znam ?!

Da bi bio genije moras biti bar malo lud. Covek koji je genije, a to ne zna, verovatno i
nije.

Odgovor na temu

Daniel011
Beograd

Član broj: 76088
Poruke: 1101
*.dynamic.sbb.rs.

ICQ: 2336441

+3 Profil

Re: Najlepši zadaci

^{30.01.2009. u 21:19 - pre 185 meseci}

Citirao bih još jednom kako je glasila prvobitna postavka zadatka:

Citat:

Koliko najvise kvadrata mozete nacrtati a dasvaki od njih ima po 2 zajednicka temena....nadam se da sam lepo objasnio ?

Izraz zajednički je sâm po sebi nedorečen, ukoliko se ne odredi sa čime je to na šta se misli zajedničko. Ovako kako je zadatak (nejasno) postavljen, jedno od rešenja koje je prikazao zzzz, a koje sam ilustrovao na sledećoj slici

je sasvim validno.

Na ovoj slici, svaki kvadrat ima tačno dva temena koja su zajednička. Zajednička su sa nekima od preostalih kvadrata na slici. Primera radi, kod kvadrata CEFG to su temena C i G:
C je zajedničko sa kvadratom ABCD, a G je zajedničko sa kvadratom GHIJ.

Ne želim da sve ovo izgleda kao teranje maka na konac, ovo je dobronamerna primedba, kako bi budući zanimljivi zadaci bili što preciznije formulisani.

Prikačeni fajlovi

Kvadrati.gif - 1.93k

Odgovor na temu

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-a-1.sezampro.yu.

+3 Profil

Re: Najlepši zadaci

^{31.01.2009. u 10:28 - pre 185 meseci}

Evo precizne formulacije jednog zadatka:

Preseci pravougaonik 4 x 9 na dva jednaka dela tako da od tih delova možeš sastaviti kvadrat.

Odgovor na temu

Daniel011
Beograd

Član broj: 76088
Poruke: 1101
*.dynamic.sbb.rs.

ICQ: 2336441

+3 Profil

Re: Najlepši zadaci

^{31.01.2009. u 12:14 - pre 185 meseci}

S obzirom da nigde nije rečeno da se pravougaonik mora preseći po pravoj liniji

, evo mog rešenja:

Prikačeni fajlovi

Pravougaonik.gif - 2.8k

Odgovor na temu

ptak 13.
Adamovic Nikola
Srbija - Nis

Član broj: 143532
Poruke: 1476
93.86.22.*

Sajt: putujsaosmehom.blogspot.c..

+284 Profil

Re: Najlepši zadaci

^{31.01.2009. u 12:26 - pre 185 meseci}

Bravo Daniel011....pretekao si me :D

Da bi bio genije moras biti bar malo lud. Covek koji je genije, a to ne zna, verovatno i
nije.

Odgovor na temu

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-1.sezampro.yu.

+3 Profil

Re: Najlepši zadaci

^{31.01.2009. u 18:18 - pre 185 meseci}

Ajd' sad 16 x 9

Odgovor na temu

ptak 13.
Adamovic Nikola
Srbija - Nis

Član broj: 143532
Poruke: 1476
93.86.22.*

Sajt: putujsaosmehom.blogspot.c..

+284 Profil

Re: Najlepši zadaci

^{31.01.2009. u 19:39 - pre 185 meseci}

Evo resenja

Nadam se da nisam pogresio u montazi

P.S. Kod mene se nesto ne vidi slika pa evo download
http://www.sendspace.com/file/ekgus3

Da bi bio genije moras biti bar malo lud. Covek koji je genije, a to ne zna, verovatno i
nije.

Odgovor na temu