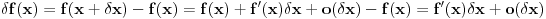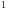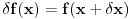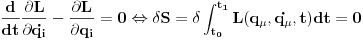
Da bi ta stacionarna vrednost duz pravog puta bila minimalna potrebno je da je
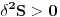 . Nisam nasao da ovo iko eksplicitno uradi. Da li postoji neki fizicki zahtev na osnovu kojeg ja mogu da zakljucim nesto o ovom ekstremu posto ne znam kako da isteram ovo sa drugom varijacijom?
. Nisam nasao da ovo iko eksplicitno uradi. Da li postoji neki fizicki zahtev na osnovu kojeg ja mogu da zakljucim nesto o ovom ekstremu posto ne znam kako da isteram ovo sa drugom varijacijom?Inace naisao sam u jednoj knjizi
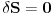 sa tacnoscu
sa tacnoscu 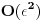
2.) Landau kaze u svojoj mehanici na 4. str
{Neka se mehanicki sistem sastoji od dva dela
 i
i  koji imaju Lagranzijane
koji imaju Lagranzijane 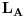 i
i 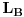 respektivno. U limesu kada rastojanje izmedju delova postane tolko veliko da se interakcija izmedju njih moze zanemariti Lagranzijan sistema ima vrednost
respektivno. U limesu kada rastojanje izmedju delova postane tolko veliko da se interakcija izmedju njih moze zanemariti Lagranzijan sistema ima vrednost 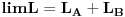 }
} Aditivnost Lagranzijana. Zanimljivo. Moze li se strogo matematicki doci do ovog zakljucka?
3.) Za funkciju
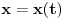 sam izveo nezavisnost variranja i diferenciranja. Nervira me malo kako je to dato u mehanikama. Kazu varijacija je infinitezimalni prirastaj fje za fiksiranu vrednost argumenta, a izvod infinitezimalni prirastaj funkcije uz infinitezimalni prirastaj argumenta pa izvod i varijacija komutiraju! Zasto?
sam izveo nezavisnost variranja i diferenciranja. Nervira me malo kako je to dato u mehanikama. Kazu varijacija je infinitezimalni prirastaj fje za fiksiranu vrednost argumenta, a izvod infinitezimalni prirastaj funkcije uz infinitezimalni prirastaj argumenta pa izvod i varijacija komutiraju! Zasto?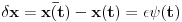

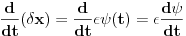
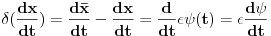
Mislim da je odavde ocigledno!
4.) Zasto za variranje vaze ista pravila kao i za diferenciranje?
Kako pokazati npr.
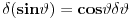
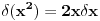 ?
?[Ovu poruku je menjao petarm dana 02.05.2008. u 11:22 GMT+1]




 Cetiri pitanja iz mehanike
Cetiri pitanja iz mehanike