Citat:
holononi: Napomena za izračunavanje trigonometrijskih funkcija razvojem u stepeni red: potrebno je ugao prevesti u radijane po obrascu x*Pi/180, gde je x ugao dat u stepenima (minuti i sekunde se moraju prevesti u stepene), Pi=3.14...
Hajmo ovako. Sinus je realna funkcija realne promenljive, rešenje Košijevog problema
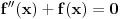
,
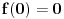
,
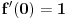
. Da bi izračunao
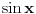
ya neko

, naravno da treba da znaš

. Stepen je ništa drugo do konstanta
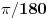
, tako da u tom slučaju treba prvo odrediti

. No, dobro, opaska za stepene je korisna za one koji bi se sapleli.
Citat:
holononi: Drugi način za približno izračunavanje vrednosti trigonometrijskih funkcija je: pomoću uglomera nacrtati zadati ugao. Povući vertikalu iz neke tačke osnovice, dobije se pravougli trougao Za sinus izračunati odnos dužina naspramne stranice i hipotenuze a za kosinus uzeti odnos dužina nalegle stranice (osnovice) i hipotenuze.
Ovo već ne bih nazvao računanjem, nego merenjem.
Citat:
holononi: Treći način se radi u drugom razredu srednje škole, pa ko nije pocepao knjige neka se podseti. Tu je opisano odredjivanje vrednosti trigonometrijskih funkcija pomoću tablica.
Pa, to opet ne bih nazvao računanjem.
Citat:
holononi: Sve rečeno važi za oštre uglove. Za tupe uglove treba koristiti kofunkcije, na primer sin(90
o ± α) = cos(α), itd.
Stepeni red važi u opštem slučaju.
Ama, dobro, slažem se sa suštinom onoga što si napisao.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.