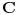[es] - Osnovni stav algebre

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8714
*.dynamic.isp.telekom.rs.

+2802 Profil

^{31.10.2013. u 14:18 - pre 140 meseci}

Kažu da ne postoji potpuno algebarski dokaz OSA. Zašto?

Šta je njegova formulacija? Da je algebarsko zatvorenje polja realnih brojeva njegovo raširenje stepena dva. A šta su to realni brojevi? Pa, to je neka strukura koja zadovoljava neke aksiome. Aksiom(e) neprekidnosti svakako nema(ju) algebarsku formulaciju, pa su algebarska sredstva ograničena na preostale aksiome, tj. aksiome uređenog polja.

E, ali te aksiome zadovoljava i polje racionalnih brojeva, čije algebarsko zatvorenje nije njegovo raširenje stepena dva jer npr. jednačina

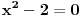nema rešenje u

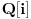. Stoga je dokaz samona osnovu tih aksioma nemoguć, pa samim tim i dokaz potpuno algebharskim sredstvima.

Ako se pak aksiom(e) neprekidnosti zamene aksiomama

1. svaki pozitivan element tog polja ima kvadratni koren u tom polju,
2. svaki polinom neparnog stepena sa koeficijentima iz tog polja ima koren u tom polju,

tj. prihvate aksiome realno zatvorenih polja, postoje potuno algebarski dokazi da je algebarsko zatvorenje takvih polja njihovo raširenej stepena dva.

Problem: Da li se uz aksiome uređenih polja može koristiti još samo jedna od navedene dve aksiome ili se moraju koristiti obe?

Ako ovo nekoga bude zanimalo, a ne bude niko rešio, mogu da postavim rešenje.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892

+332 Profil

Re: Osnovni stav algebre

^{31.10.2013. u 14:48 - pre 140 meseci}

Sta fali dokazu teoreme iz Gojkove knjige:

Teorema. Polje

je algebarski zatvoreno. I uopste, ako neko polje

karakteristike nula nema pravih rasirenja neparnog stepena, njegovo kvadratno rasirenje

je i algebarski zatvoreno, ako i samo ako nema rasirenja stepena dva.

U dokazu se koristi teorija Galua i prva Silovljeva teorema.

Iskreno, nisam se nesto udubljivao u tvoj post, to diranje mecke me nikada nije puno zanimalo iskreno, al koliko vidim, za ovaj dokaz koji sam spomenuo se koriste obe aksiome koje si naveo.

Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8714
*.dynamic.isp.telekom.rs.

+2802 Profil

Re: Osnovni stav algebre

^{31.10.2013. u 15:11 - pre 140 meseci}

Ma, ne fali mu ništa, samo što nije potpuno algebarski jer se poziva na 1 i 2, što prethodno izvodi nealgebarski iz aksiome supremuma.

Nije poenta problema u "algebarskoj čistoći", već u tome da li iz aksioma uređenog polja i jedne od aksioma 1 i 2 sledi da je kvadratno raširenje svakog takvog polja algebarski zatvoreno ili ne sledi?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892

+332 Profil

Re: Osnovni stav algebre

^{31.10.2013. u 15:32 - pre 140 meseci}

Mislim da ne moze. To ovako intuitivno. Al ne bih umeo da pokazem.

Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8714
*.dynamic.isp.telekom.rs.

+2802 Profil

Re: Osnovni stav algebre

^{31.10.2013. u 15:55 - pre 140 meseci}

Odgovor je tačan. No, da vidimo hoće li se javiti još neko.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.uns.ac.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Osnovni stav algebre

^{31.10.2013. u 16:01 - pre 140 meseci}

Moguće da nešto propuštam, ali zar nije prilično jednostavno? Čini mi se da je dovoljno krenuti od polja

i ubaciti još „nešto“ unutra na taj način da se u jednoj odnosno drugoj varijanti dobije polje koje zadovoljava prvu predloženu aksiomu odnosno drugu predloženu aksiomu, a ne zadovoljava traženi zaključak. Pritom meni deluje prilično očigledno šta je to „nešto“ što ćemo ubaciti u prvom, odnosno drugom slučaju (no ne isključujem mogućnost greške). Zasad neću eksplicitno da napišem u slučaju da neko želi da razmisli još malo.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8714
*.3gnet.mts.telekom.rs.

+2802 Profil

Re: Osnovni stav algebre

^{31.10.2013. u 21:38 - pre 140 meseci}

Da, treba naći dva uređena polja čija algebarska zatvorenja nisu njihova kvadratna proširenja, pri čemu prvo treba da zadovolji prvu aksiomu, a drugo drugu.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8714
*.dynamic.isp.telekom.rs.

+2802 Profil

Re: Osnovni stav algebre

^{02.11.2013. u 08:49 - pre 140 meseci}

Ima li zainteresovanih?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu