Postupak je zapravo vrlo jednostavan, i poznat ti je vec pod imenom "metoda suprotnih koeficijenata".. ali ja cu dati sve od sebe da ga zakompliciram:) kako bi eventualno ubuduce lakse presla na rjesavanje sistema od vise jednacina s vise nepoznatih..
Neka je zadan sistem jednacina s dvije nepoznate:
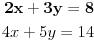
- Korak 1:
Pomnozimo prvu jednacinu s
.
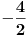
Sistem sad izgleda ovako:
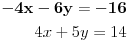
- Korak 2:
PRIBROJIMO li gornju jednacinu donjoj, sistem ce izgledati ovako:
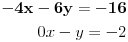
(primijetimo da nakon "pribrajanja" gornja jednacina ostaje ista, a donja se promijenila..)
Sta smo dobili? - pogledamo li drugu jednadzbu, vidimo da nam nepoznanicu x mnozi nula, pa zapravo druga jednadzba izgleda ovako:
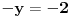
Dakle, nasim postupkom smo ELIMINIRALI jednu nepoznatu!, pa iz druge jednacine jasno citamo da je
.
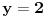
- Korak 3:
Uvrstimo li sad
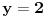
u prvu jednadzbu (bilo polaznu, bilo onu koju smo dobilli nakon mnozenja s
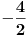
), dobijamo:
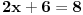
, odnosno
. (Uvrstio sam u polaznu jednacinu)
................
To bi bilo to, a sad malo pojasnjenja sto smo napravili:
Vidimo da smo do rjesenja sistema jednacina (uredjen par
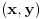
) dosli tako sto smo zadani sistem transformirali u neki jednostavniji, iz kojeg smo lakse dobili rjesenje. E sad to transformiranje nije bogom dano, nego postoje matematicki teoremi (tj pravila) koja nam osiguravaju da razlikujemo ispravne postupke transformiranja od neispravnih.
"Pravilnim" transformiranjem, mi zapravo svodimo zadani sistem u njemu EKVIVALENTAN sistem, najcesce u sto jednostavniji takav. (Kazemo da su dva sistema jednacina ekvivalentna ako je svako rjesenje prvog ujedno rjesenje i drugog, i obratno).
Npr, sva tri gore navedena sistema su ekvivalentna, jer smo ih dobili "pravilnim" transformiranjem.
Navedimo sad tocno koje su to "pravilne" transformacije jednacina sistema koje smijemo koristiti, da bi sistem transformirali u njemu ekvivalentan, tj u onaj koji ima rjesenje kao i polazni:
1) pomnoziti bilo koju jednacinu brojem razlicitim od nule
2) PRIBROJITI jednu jednacinu drugoj.
Ova dva pravila se u praksi obicno primjenjuju u jednom koraku, tj (u mislima) najprije pomnozimo prvu jednacinu nekim brojem (kao sto smo gore ucinili s
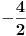
), te tako "pomnozenu" pribrajamo drugoj jednacini. Navedoh da mnozenje obavimo "u mislima" jer je mnogo jednostavnije da prva jednadzba pri tom ostane ista, (a ne pomnozena nekim (ruznim) razlomkom).
(Npr, mada u mom primjeru to nije tako ocito, ipak opcenito bi bilo jednostavnije da sam Korak 1 napravio u mislima, i u sistemu pod Korakom 2 ostavio prvu jednacinu istu kao i polaznu).
Ostaje jos samo pitanje S KOJIM BROJEM mnoziti prvu jednacinu, da bi osigurali da ce nakon pribrajanja, sustav biti doista JEDNOSTAVNIJI?
Pogledajmo jos jednom polazni sustav:
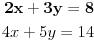
Prvu jednacinu smo mnozili s
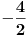
. Primijetimo da je u brojniku broj 4 (tj koeficijent uz x iz druge jednadzbe), a u nazivniku broj 2 (tj koeficijent uz x iz jednadzbe koju mnozimo, u nasem slucaju, iz prve.), a ne zanemarimo ni "minus" ispred razlomacke crte!
Zasto smo odabrali bas te brojeve i stavili ih u razlomak, dodijelivsi mu pri tom i predznak minus, pa mnozili njime? - Pa jednostavno zato sto cemo nakon sto pomnozimo prvu jednacinu s BAS tim razlomkom, i pribrojimo je drugoj jednacini, ELIMINIRATI jednu nepoznatu!, kao sto smo gore i vidjeli.
Dakle poanta, i kljuc rjesavanja Gausovom metodom eliminacije, je da se u danom sistemu jednacina:
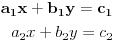
jedna jednacina ( u nasem slucaju, i najcesce, prva) u mislima pomnozi s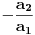 
, i pomnozena pribroji drugoj, pri cemu dolazi do ELIMINACIJE nepoznate ( u nasem slucaju x), te se lako cita rjesenje druge nepoznate (y).
A onda je lako uvrstiti vrijednost izracunate nepoznate y u prvu jednacinu i izracunati preostalu nepoznatu x.
Primijetimo, naravno ako bismo zeljeli eliminirati nepoznatu y, tada cemo prvu jednacinu mnoziti s
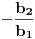
, i pribrojiti je drugoj, iz koje cemo onda direktno citati koliki je x.. pa ga uvrstiti u prvu jednacinu i dobiti y.
Dodajmo jos da se Gausova metoda u opcenitom obliku moze primijeniti na svaki sistem linearnih jednacina, a bilo bi zgodno jos malo diskutirati o (ne)proturjecnosti i (ne)odredjenosti sistema..
ali to nisi pitala:)
Bem mu, sad na tebe potrosih svoje omiljeno vrijeme rezervirano za surfanje porno stranicama..
Sistem linearnih jednacina sa dve nepoznate
Registrovani: 1 ( Ivan Dimkovic )
Re: Sistem linearnih jednacina sa dve nepoznate
