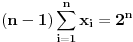Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.

Matrice/ Linerarne forme/ Sistemi linearnih jednacina sa parametrima

[es] :: Matematika :: Matrice/ Linerarne forme/ Sistemi linearnih jednacina sa parametrima

[ Pregleda: 3013 | Odgovora: 3 ]

 Postavi temu Odgovori

Autor
Pretraga teme: Traži
Markiranje Štampanje RSS

muhay
Muhamed Halilovic
Sarajevo

Član broj: 23634
Poruke: 13
*.as-sa01.europronet.ba



Profil

icon Matrice/ Linerarne forme/ Sistemi linearnih jednacina sa parametrima31.03.2004. u 13:43

...Mozeli neko preporuciti kakave dobre linkove/literaturu vezane za sisteme linearnih jednacina, i koristenje razlicitih metoda za iznalazenja rijesenja (Gausov metod, koristenje Kronecker-Kaplejievog stava i slicno)...Da li neko zna mozda da rijesi slijedeca dva zadatka:

a) Rijesiti sistem linearnih jednacina
X2+X3+...+Xn=(n nad 1)
X1+X3+...+Xn=(n nad 2)
- - - - - - - - - - - - - -
X1+X2+...+Xn-1=(n nad n)

b) Odrediti parametar d, tako da sistem
2X+6Y+(d+6)Z=0, -X+7Y+5Z=0, dX+5Y+13Z=0
ima netrivijalna rijesenja, a zatim naci ta rjesenja.
Odrediti jednacinu ravni koja sadrzi sva netrivijalna rjesenja tog sistema, te tacku A simetricnu tacki M(1,-2,0) u odnosu na tu ravan
...Biti ili ne biti, pitanje je sad!
Ja bi da bijem...
31.03.2004. u 13:43 

filmil
Filip Miletić
Oce Technologies B.V., inženjer hardvera
Arcen, NL

Član broj: 243
Poruke: 2114
*.et.tudelft.nl

Jabber: filmil@jabber.org
ICQ: 36601391


Profil

icon Re: Matrice/ Linerarne forme/ Sistemi linearnih jednacina sa parametrima31.03.2004. u 17:49
Što se tiče prvog zadatka, valjalo bi verovatno sabrati sve jednačine. Dobija se
(priseti se binomnih koeficijenata), odakle se lako dobija vrednost za sumu svih promenljivih deljenjem sa . Zatim promenljivu sračunaš oduzimajući jednačinu broj i od zbira.

f
31.03.2004. u 17:49 

Nedeljko
Nedeljko Stefanovic

Član broj: 314
Poruke: 2933
*.rcub.bg.ac.yu



Profil

icon Re: Matrice/ Linerarne forme/ Sistemi linearnih jednacina sa parametrima06.04.2004. u 16:32
Filip se malo prešao, jer zbir je 2^n-1 budući da sabirka (n nad 0) nema. No, ostatak uputstva je dobar, pa je x_i=(2^n-1)/(n-1)-(n nad i).

No, što se tiče drugog, sasvim je elementaran budući da kvadratan homogen sistem linearnih jednačina (dakle nxn) ima netrivijalno rešenje ako i samo ako mu jed eterminanta jednaka nuli. To se u ovom slučaju svodi na kvadratnu jednačinu po d. Potom se te vrednosti zamene u sistemu i reši se sistem u svakom od ta dva slučaja.

By the way, kako se ubacuju LaTeX formule u ove poruke? Ne treba mi uputstvo za LaTeX, već samo za ubacivanje formula u poruke na ovom forumu.
06.04.2004. u 16:32 

leka
Dejan Lekić
senior software engineer, 3Developers Ltd.
London, UK

Član broj: 234
Poruke: 2530
*.racasse.se

Sajt: dejan.lekic.org


Profil

icon Re: Matrice/ Linerarne forme/ Sistemi linearnih jednacina sa parametrima06.04.2004. u 16:55
Pa kao i sve ostalo:
Code:
[te><]n/2[/te><]
. Naravno umesto "><" treba kucati "x"...
Dejan Lekic
software engineer, MySQL/PgSQL DBA, sysadmin
06.04.2004. u 16:55 

[es] :: Matematika :: Matrice/ Linerarne forme/ Sistemi linearnih jednacina sa parametrima

[ Pregleda: 3013 | Odgovora: 3 ]

 Postavi temu Odgovori

Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.