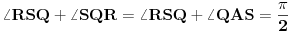Neka ja P srediste osnovice BC jednakokrakog trougla ABC i Q podnozje upravne iz tacke P na kraku AC tog trougla.Ako je S srediste PQ dokazati da je AS((T)^-1)BQ.
Ja nisam uspio da ga uradim na ispitu mada sam bio mamuran i neispavan, ali me bas interesuje rijesenje.
Hvala unaprijed za rijesenje.
Reko mi tvoj brat da studiras za programatora!




 Zadatak iz geometrije sa septembarskog ispitnog roka.
Zadatak iz geometrije sa septembarskog ispitnog roka.